Advertisements
Advertisements
Question
In ΔPQR, LM = MN, QM = MR and ML and MN are perpendiculars on PQ and PR respectively. Prove that PQ = PR.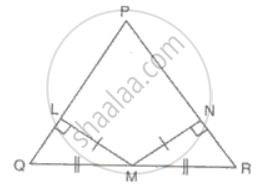
Solution
In ΔQLM and ΔRNM
QM = MR
LM = MN
∠QLM = ∠RNM = 90°
Therefore, ΔQLM ≅ ΔRNM ...(RHS criteria)
Hence, QL = RN ..........(i)
Join PM
In ΔPLM and ΔPNM and
PM = PM ...(common)
LM = MN
∠PLM = ∠PNM = 90°
Therefore, ΔPLM ≅ ΔPNM ...(RHS criteria)
Hence, PL = PN ..........(ii)
From (i) and (ii)
PQ = PR.
APPEARS IN
RELATED QUESTIONS
In two right triangles one side an acute angle of one are equal to the corresponding side and angle of the othe Prove that the triangles are congruent.
Prove that the sum of three altitudes of a triangle is less than the sum of its sides.
In the given figure, if AE || DC and AB = AC, the value of ∠ABD is
In the following example, a pair of triangles is shown. Equal parts of triangle in each pair are marked with the same sign. Observe the figure and state the test by which the triangle in each pair are congruent.

By ______ test
ΔXYZ ≅ ΔLMN
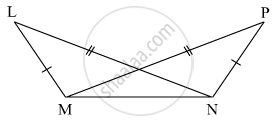
As shown in the following figure, in ΔLMN and ΔPNM, LM = PN, LN = PM. Write the test which assures the congruence of the two triangles. Write their remaining congruent parts.
The following figure has shown a triangle ABC in which AB = AC. M is a point on AB and N is a point on AC such that BM = CN.
Prove that: (i) BN = CM (ii) ΔBMC≅ΔCNB

A is any point in the angle PQR such that the perpendiculars drawn from A on PQ and QR are equal. Prove that ∠AQP = ∠AQR.
In ΔABC, AB = AC. D is a point in the interior of the triangle such that ∠DBC = ∠DCB. Prove that AD bisects ∠BAC of ΔABC.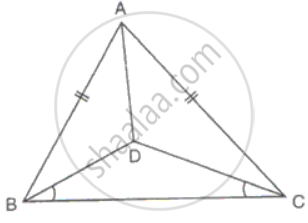
The top and bottom faces of a kaleidoscope are congruent.
Without drawing the triangles write all six pairs of equal measures in the following pairs of congruent triangles.
∆STU ≅ ∆DEF
