Advertisements
Advertisements
Question
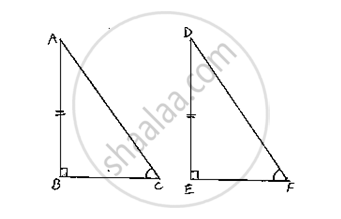
In two right triangles one side an acute angle of one are equal to the corresponding side and angle of the othe Prove that the triangles are congruent.
Solution
Given that, in two right triangles one side and acute angle of one are equal to the corresponding side and angles of the other.
We have to prove that the triangles are congruent. Let us consider two right triangles such that
∠B = ∠C = 90° ........(1)
AB = DE ........(2)
∠C = ∠F ........(3)
Now observe the two triangles ABC and DEF
∠.C = ∠F [From (3)]
∠B = ∠E [From (1)]
and AB = DE [From (2)]
So, by AAS congruence criterion, we have
ΔABC ≅ ΔDEF
∴The two triangles are congruent Hence proved
APPEARS IN
RELATED QUESTIONS
In ΔTPQ, ∠T = 65°, ∠P = 95° which of the following is a true statement?
In the pair of triangles given below, the parts shown by identical marks are congruent. State the test and the one-to-one correspondence of vertices by which the triangles in the pair are congruent, the remaining congruent parts.
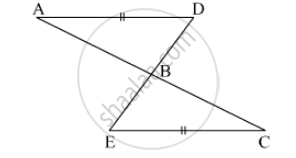
In the adjacent figure, seg AD ≌ seg EC Which additional information is needed to show that ∆ ABD and ∆ EBC will be congruent by A-A-S test?
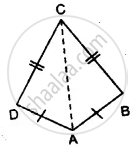
Prove that:
(i) ∆ ABC ≅ ∆ ADC
(ii) ∠B = ∠D
(iii) AC bisects angle DCB
Which of the following pairs of triangles are congruent? Give reasons
ΔABC;(BC = 5cm,AC = 6cm,∠C = 80°);
ΔXYZ;(XZ = 6cm,XY = 5cm,∠X = 70°).
Which of the following pairs of triangles are congruent? Give reasons
ΔABC;(∠B = 90°,BC = 6cm,AB = 8cm);
ΔPQR;(∠Q = 90°,PQ = 6cm,PR = 10cm).
In a triangle ABC, if D is midpoint of BC; AD is produced upto E such as DE = AD, then prove that:
a. DABD andDECD are congruent.
b. AB = EC
c. AB is parallel to EC
In ΔABC, AB = AC and the bisectors of angles B and C intersect at point O.Prove that BO = CO and the ray AO is the bisector of angle BAC.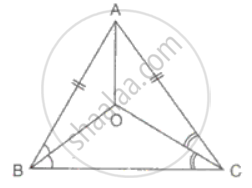
In the figure, AC = AE, AB = AD and ∠BAD = ∠EAC. Prove that BC = DE.
Is it possible to construct a triangle with lengths of its sides as 4 cm, 3 cm and 7 cm? Give reason for your answer.
