Advertisements
Advertisements
Question
In ΔTPQ, ∠T = 65°, ∠P = 95° which of the following is a true statement?
Options
PQ < TP
PQ < TQ
TQ < TP < PQ
PQ < TP < TQ
Solution
PQ < TQ
Explanation:
∠Q = 180° – (95° + 65°)
∠Q = 20°
∴ ∠Q < ∠T < ∠P
∴ PT < PQ < TQ
APPEARS IN
RELATED QUESTIONS
If ΔDEF ≅ ΔBCA, write the part(s) of ΔBCA that correspond to `bar(DF)`
In Fig. 10.22, the sides BA and CA have been produced such that: BA = AD and CA = AE.
Prove that segment DE || BC.
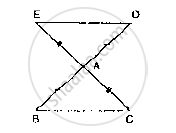
In two right triangles one side an acute angle of one are equal to the corresponding side and angle of the othe Prove that the triangles are congruent.
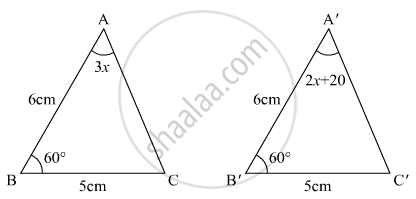
In the given figure, the measure of ∠B'A'C' is
In the following diagram, ABCD is a square and APB is an equilateral triangle.
(i) Prove that: ΔAPD≅ ΔBPC
(ii) Find the angles of ΔDPC.
State, whether the pairs of triangles given in the following figures are congruent or not:
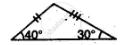
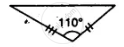
State, whether the pairs of triangles given in the following figures are congruent or not:

In triangles ABC and PQR, ∠A = ∠Q and ∠B = ∠R. Which side of ∆PQR should be equal to side AB of ∆ABC so that the two triangles are congruent? Give reason for your answer.
In triangles ABC and PQR, ∠A = ∠Q and ∠B = ∠R. Which side of ∆PQR should be equal to side BC of ∆ABC so that the two triangles are congruent? Give reason for your answer.
It is given that ∆ABC ≅ ∆RPQ. Is it true to say that BC = QR? Why?
