Advertisements
Advertisements
Question
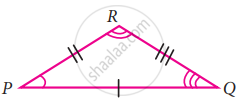
It is given that ∆ABC ≅ ∆RPQ. Is it true to say that BC = QR? Why?
Solution
No, we know that two triangles are congruent, if the sides and angles of one triangle are equal to the corresponding side and angles of other triangle.
Here ΔABC ≅ ΔRPQ
AB = RP, BC = PQ and AC = RQ
Hence, it is not true to say that BC = QR.
APPEARS IN
RELATED QUESTIONS
If ΔDEF ≅ ΔBCA, write the part(s) of ΔBCA that correspond to ∠F
In a squared sheet, draw two triangles of equal areas such that
The triangles are congruent.
What can you say about their perimeters?
In ΔTPQ, ∠T = 65°, ∠P = 95° which of the following is a true statement?
In the pair of triangles in the following figure, parts bearing identical marks are congruent. State the test and the correspondence of vertices by the triangle in pairs is congruent.

The following figure has shown a triangle ABC in which AB = AC. M is a point on AB and N is a point on AC such that BM = CN.
Prove that: (i) BN = CM (ii) ΔBMC≅ΔCNB

In a triangle ABC, if D is midpoint of BC; AD is produced upto E such as DE = AD, then prove that:
a. DABD andDECD are congruent.
b. AB = EC
c. AB is parallel to EC
In the figure, BC = CE and ∠1 = ∠2. Prove that ΔGCB ≅ ΔDCE.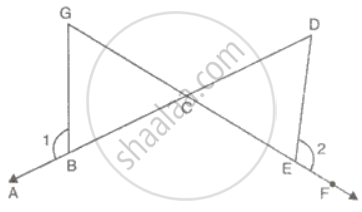
In the figure, AB = EF, BC = DE, AB and FE are perpendiculars on BE. Prove that ΔABD ≅ ΔFEC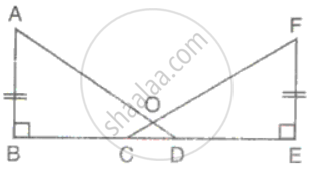
Prove that in an isosceles triangle the altitude from the vertex will bisect the base.
If the given two triangles are congruent, then identify all the corresponding sides and also write the congruent angles