Advertisements
Advertisements
Question
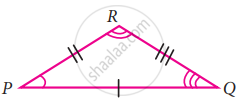
In the pair of triangles in the following figure, parts bearing identical marks are congruent. State the test and the correspondence of vertices by the triangle in pairs is congruent.

Solution
The two triangles are congruent by the SSS test, in the correspondence HEG ↔ FGE.
RELATED QUESTIONS
Complete the congruence statement:
ΔBCA ≅?
ΔQRS ≅?
In a squared sheet, draw two triangles of equal areas such that
The triangles are congruent.
What can you say about their perimeters?
In two right triangles one side an acute angle of one are equal to the corresponding side and angle of the othe Prove that the triangles are congruent.
CDE is an equilateral triangle formed on a side CD of a square ABCD. Show that ΔADE ≅ΔBCE.
In the given figure, X is a point in the interior of square ABCD. AXYZ is also a square. If DY = 3 cm and AZ = 2 cm, then BY =

From the information shown in the figure, state the test assuring the congruence of ΔABC and ΔPQR. Write the remaining congruent parts of the triangles.
In the following diagram, AP and BQ are equal and parallel to each other.

Prove that:
(i) ΔAOP≅ ΔBOQ.
(ii) AB and PQ bisect each other.
O is any point in the ΔABC such that the perpendicular drawn from O on AB and AC are equal. Prove that OA is the bisector of ∠BAC.
∆ABC and ∆PQR are congruent under the correspondence:
ABC ↔ RQP
Write the parts of ∆ABC that correspond to
(i) `bar"PQ"`
(ii)∠Q
(iii) `bar"RP"`
If the given two triangles are congruent, then identify all the corresponding sides and also write the congruent angles