Advertisements
Advertisements
Question
O is any point in the ΔABC such that the perpendicular drawn from O on AB and AC are equal. Prove that OA is the bisector of ∠BAC.
Solution
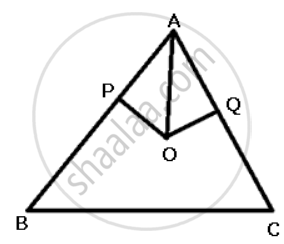
In ΔPOA and ΔQOA
∠OPA = ∠OQA = 90°
OP = OQ ...(given)
AO = AO
Therefore, ΔPOA ≅ ΔQOA ...(SSA criteria)
Hence, ∠PAO = ∠QAO
Thus, OA bisects ∠BAC.
APPEARS IN
RELATED QUESTIONS
Complete the congruence statement:
ΔBCA ≅?
ΔQRS ≅?
CDE is an equilateral triangle formed on a side CD of a square ABCD. Show that ΔADE ≅ΔBCE.
ΔPQR and ΔABC is not congruent to ΔRPQ, then which of the following is not true:
In the following figure, OA = OC and AB = BC.

Prove that: AD = CD
State, whether the pairs of triangles given in the following figures are congruent or not:
In ΔABC, AB = AC, BM and Cn are perpendiculars on AC and AB respectively. Prove that BM = CN.
∆ABC and ∆PQR are congruent under the correspondence:
ABC ↔ RQP
Write the parts of ∆ABC that correspond to
(i) `bar"PQ"`
(ii)∠Q
(iii) `bar"RP"`
Given that ∆ABC ≅ ∆DEF List all the corresponding congruent sides
Is it possible to construct a triangle with lengths of its sides as 4 cm, 3 cm and 7 cm? Give reason for your answer.
The congruent figures super impose each other completely.
