Advertisements
Advertisements
प्रश्न
O is any point in the ΔABC such that the perpendicular drawn from O on AB and AC are equal. Prove that OA is the bisector of ∠BAC.
उत्तर
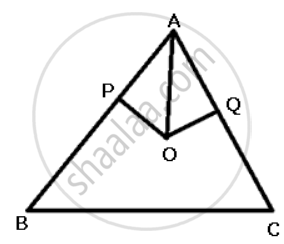
In ΔPOA and ΔQOA
∠OPA = ∠OQA = 90°
OP = OQ ...(given)
AO = AO
Therefore, ΔPOA ≅ ΔQOA ...(SSA criteria)
Hence, ∠PAO = ∠QAO
Thus, OA bisects ∠BAC.
APPEARS IN
संबंधित प्रश्न
If ΔDEF ≅ ΔBCA, write the part(s) of ΔBCA that correspond to ∠E
Mark the correct alternative in each of the following:
If ABC ≅ ΔLKM, then side of ΔLKM equal to side AC of ΔABC is
ABC is an isosceles triangle such that AB = AC and AD is the median to base BC. Then, ∠BAD =
In the given figure, X is a point in the interior of square ABCD. AXYZ is also a square. If DY = 3 cm and AZ = 2 cm, then BY =

In the pair of triangles in the following figure, parts bearing identical marks are congruent. State the test and the correspondence of vertices by the triangle in pairs is congruent.
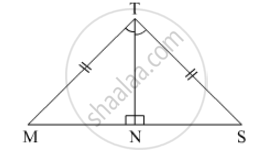
In the following figure, OA = OC and AB = BC.
Prove that:
(i) ∠AOB = 90o
(ii) ΔAOD ≅ ΔCOD
(iii) AD = CD
The following figure has shown a triangle ABC in which AB = AC. M is a point on AB and N is a point on AC such that BM = CN.
Prove that: (i) AM = AN (ii) ΔAMC ≅ ΔANB

State, whether the pairs of triangles given in the following figures are congruent or not:

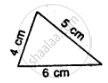
Which of the following pairs of triangles are congruent? Give reasons
ΔABC;(AB = 5cm,BC = 7cm,CA = 9cm);
ΔKLM;(KL = 7cm,LM = 5cm,KM = 9cm).
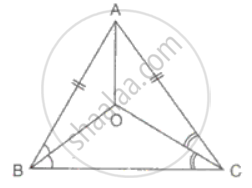
In ΔABC, AB = AC and the bisectors of angles B and C intersect at point O.Prove that BO = CO and the ray AO is the bisector of angle BAC.