Advertisements
Advertisements
प्रश्न
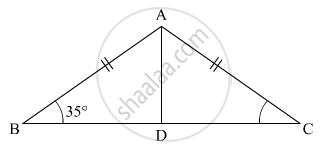
ABC is an isosceles triangle such that AB = AC and AD is the median to base BC. Then, ∠BAD =
पर्याय
55°
70°
35°
110°
उत्तर
It is given that ∠B = 35°, AB=AC and Ad is the median of BC

We know that in isosceles triangle the median from he vertex to the unequal side divides it into two equal part at right angle.
Therefore,
∠ADB = 90°
∠B = ∠ADB + ∠A= 180° (Property of triangle)
35° + 90° +∠A = 180°
∠A = 180° - 125°
∠A = 55°
APPEARS IN
संबंधित प्रश्न
CDE is an equilateral triangle formed on a side CD of a square ABCD. Show that ΔADE ≅ΔBCE.
In ΔPQR ≅ ΔEFD then ED =
Observe the information shown in pair of triangle given below. State the test by which the two triangles are congruent. Write the remaining congruent parts of the triangles.
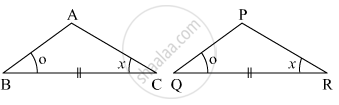
From the information shown in the figure,
In ΔABC and ΔPQR
∠ABC ≅ ∠PQR
seg BC ≅ seg QR
∠ACB ≅ ∠PRQ
∴ ΔABC ≅ ΔPQR ...`square` test
∴ ∠BAC ≅ `square` ...corresponding angles of congruent triangles.
`{:("seg AB" ≅ square),("and" square ≅ "seg PR"):}}` ...corresponding sides of congruent triangles
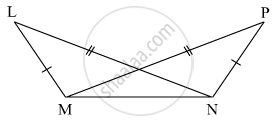
As shown in the following figure, in ΔLMN and ΔPNM, LM = PN, LN = PM. Write the test which assures the congruence of the two triangles. Write their remaining congruent parts.
The following figure has shown a triangle ABC in which AB = AC. M is a point on AB and N is a point on AC such that BM = CN.
Prove that: (i) BN = CM (ii) ΔBMC≅ΔCNB

Which of the following pairs of triangles are congruent? Give reasons
ΔABC;(∠B = 70°,BC = 6cm,∠C = 50°);
ΔXYZ;(∠Z = 60°,XY = 6cm,∠X = 70°).
In ΔABC, AB = AC, BM and Cn are perpendiculars on AC and AB respectively. Prove that BM = CN.
In triangles ABC and DEF, AB = FD and ∠A = ∠D. The two triangles will be congruent by SAS axiom if ______.
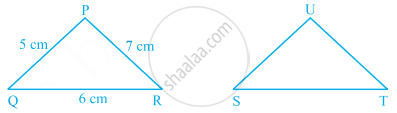
If ∆PQR is congruent to ∆STU (see figure), then what is the length of TU?
Without drawing the triangles write all six pairs of equal measures in the following pairs of congruent triangles.
∆YZX ≅ ∆PQR
