Advertisements
Advertisements
प्रश्न
D, E, F are the mid-point of the sides BC, CA and AB respectively of ΔABC. Then ΔDEF is congruent to triangle
पर्याय
ABC
AEF
BFD, CDE
AFE, BFD, CDE
उत्तर
It is given that D, E and Fare the mid points of the sides BC , CA and AB respectively of ΔABC
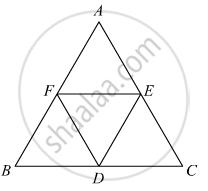
FE =BD (By mid point theorem)
BD = DC (As it is mid point)
Now in ΔAFE and ΔDFE
FE(Common)
DF = AE (Mid point)
AF = DE (Mid point)
⇒ ΔFED ≅ ΔBFD
⇒ ΔDFE ≅ ΔDCE
Hence (d)
ΔDFE ≅ AFE
≅ BFD
≅ CDE
APPEARS IN
संबंधित प्रश्न
In right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see the given figure). Show that:
- ΔAMC ≅ ΔBMD
- ∠DBC is a right angle.
- ΔDBC ≅ ΔACB
- CM = `1/2` AB

You want to show that ΔART ≅ ΔPEN,
If you have to use SSS criterion, then you need to show
1) AR =
2) RT =
3) AT =

In Δ ABC, ∠B = 35°, ∠C = 65° and the bisector of ∠BAC meets BC in P. Arrange AP, BP and CP in descending order.
In two congruent triangles ABC and DEF, if AB = DE and BC = EF. Name the pairs of equal angles.
In the given figure, ABC is an isosceles triangle whose side AC is produced to E. Through C, CD is drawn parallel to BA. The value of x is

If the following pair of the triangle is congruent? state the condition of congruency :
In Δ ABC and Δ DEF, AB = DE, BC = EF and ∠ B = ∠ E.
A triangle ABC has ∠B = ∠C.
Prove that: The perpendiculars from the mid-point of BC to AB and AC are equal.
In the following figure, AB = AC and AD is perpendicular to BC. BE bisects angle B and EF is perpendicular to AB.
Prove that : ED = EF

In the following figure, AB = EF, BC = DE and ∠B = ∠E = 90°.
Prove that AD = FC.
ABC is a right triangle with AB = AC. Bisector of ∠A meets BC at D. Prove that BC = 2AD.
