Advertisements
Advertisements
Question
D, E, F are the mid-point of the sides BC, CA and AB respectively of ΔABC. Then ΔDEF is congruent to triangle
Options
ABC
AEF
BFD, CDE
AFE, BFD, CDE
Solution
It is given that D, E and Fare the mid points of the sides BC , CA and AB respectively of ΔABC
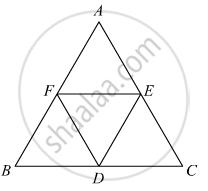
FE =BD (By mid point theorem)
BD = DC (As it is mid point)
Now in ΔAFE and ΔDFE
FE(Common)
DF = AE (Mid point)
AF = DE (Mid point)
⇒ ΔFED ≅ ΔBFD
⇒ ΔDFE ≅ ΔDCE
Hence (d)
ΔDFE ≅ AFE
≅ BFD
≅ CDE
APPEARS IN
RELATED QUESTIONS
You have to show that ΔAMP ≅ AMQ.
In the following proof, supply the missing reasons.
| Steps | Reasons | ||
| 1 | PM = QM | 1 | ... |
| 2 | ∠PMA = ∠QMA | 2 | ... |
| 3 | AM = AM | 3 | ... |
| 4 | ΔAMP ≅ ΔAMQ | 4 | ... |

In a triangle ABC, D is mid-point of BC; AD is produced up to E so that DE = AD.
Prove that :
(i) ΔABD and ΔECD are congruent.
(ii) AB = CE.
(iii) AB is parallel to EC
In a triangle ABC, D is mid-point of BC; AD is produced up to E so that DE = AD. Prove that:
AB is parallel to EC.
A triangle ABC has ∠B = ∠C.
Prove that: The perpendiculars from the mid-point of BC to AB and AC are equal.
From the given diagram, in which ABCD is a parallelogram, ABL is a line segment and E is mid-point of BC.
Prove that: AB = BL.
In the given figure: AB//FD, AC//GE and BD = CE;
prove that:
- BG = DF
- CF = EG

In ∆ABC, AB = AC. Show that the altitude AD is median also.
In the following figure, AB = AC and AD is perpendicular to BC. BE bisects angle B and EF is perpendicular to AB.
Prove that : ED = EF

In the following diagram, AP and BQ are equal and parallel to each other. 
Prove that: AB and PQ bisect each other.
A point O is taken inside a rhombus ABCD such that its distance from the vertices B and D are equal. Show that AOC is a straight line.
