Advertisements
Advertisements
Question
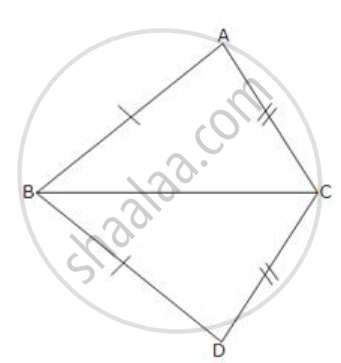
A point O is taken inside a rhombus ABCD such that its distance from the vertices B and D are equal. Show that AOC is a straight line.
Solution

In ΔAOD and ΔAOB,
AD = AB ...(given)
AO = AO ...(Common)
OD = OB ...(given)
⇒ ΔAOD ≅ ΔAOB ...(by SSS congruence criterion)
⇒ ∠AOD = ∠AOB ...(c.p.c.t.) ...(i)
Similarly, ΔDOC ≅ ΔBOC
⇒ ∠DOC = ∠BOC ...(c.p.c.t.) ...(ii)
But, ∠AOB + ∠AOD + ∠COD + ∠BOC = 4 Right angles ...[ Sum of the angles at a point is 4 Right angles ]
⇒ 2∠AOD + 2∠COD = 4 Right angles ....[ Using (i) and (ii) ]
⇒ ∠AOD + ∠COD = 2 Right angles
⇒ ∠AOD + ∠COD = 180°
⇒ ∠AOD and ∠COD form a linear pair.
⇒ AO and OC are in the same straight line.
⇒ AOC is a straight line.
APPEARS IN
RELATED QUESTIONS
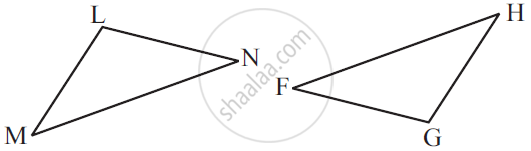
Which congruence criterion do you use in the following?
Given: ∠MLN = ∠FGH
∠NML = ∠GFH
ML = FG
So, ΔLMN ≅ ΔGFH
You want to show that ΔART ≅ ΔPEN,
If you have to use SSS criterion, then you need to show
1) AR =
2) RT =
3) AT =

In Fig. 10.99, AD ⊥ CD and CB ⊥. CD. If AQ = BP and DP = CQ, prove that ∠DAQ = ∠CBP.

Prove that the perimeter of a triangle is greater than the sum of its altitudes.
In two triangles ABC and DEF, it is given that ∠A = ∠D, ∠B = ∠E and ∠C =∠F. Are the two triangles necessarily congruent?
From the given diagram, in which ABCD is a parallelogram, ABL is a line segment and E is mid-point of BC.
Prove that: AB = BL.
In the given figure, AB = DB and Ac = DC.
If ∠ ABD = 58o,
∠ DBC = (2x - 4)o,
∠ ACB = y + 15o and
∠ DCB = 63o ; find the values of x and y.
In the given figure: AB//FD, AC//GE and BD = CE;
prove that:
- BG = DF
- CF = EG

In the following figure, ∠A = ∠C and AB = BC.
Prove that ΔABD ≅ ΔCBE. 
Which of the following is not a criterion for congruence of triangles?
