Advertisements
Advertisements
Question
In the given figure: AB//FD, AC//GE and BD = CE;
prove that:
- BG = DF
- CF = EG

Solution
In the given figure AB || FD,
⇒ ∠ABC =∠FDC
Also AC || GE,
⇒ ∠ACB = ∠GEB
Consider the two triangles ΔGBE and ΔFDC
∠B = ∠D ...(Corresponding angle)
∠C = ∠E ...(Corresponding angle)
Also given that
BD = CE
⇒ BD + DE = CE + DE
⇒ BE = DC
∴ By Angle-Side-Side-Angle criterion of congruence
ΔGBE ≅ ΔFDC
∴ `"GB"/"FD" = "BE"/"DC" = "GE"/"FC"`
But BE = DC
⇒ `"BE"/"DC" = "BE"/"BE"` = 1
∴ `"GB"/"FD" = "BE"/"DC"` = 1
⇒ GB = FD
∴ `"GE"/"FC" = "BE"/"DC"` = 1
⇒ GE = FC
APPEARS IN
RELATED QUESTIONS
In ΔABC, ∠A = 30°, ∠B = 40° and ∠C = 110°
In ΔPQR, ∠P = 30°, ∠Q = 40° and ∠R = 110°
A student says that ΔABC ≅ ΔPQR by AAA congruence criterion. Is he justified? Why or why not?
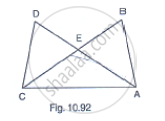
In Fig. 10.92, it is given that AB = CD and AD = BC. Prove that ΔADC ≅ ΔCBA.
ABC is an isosceles triangle in which AB = AC. BE and CF are its two medians. Show that BE = CF.
The given figure shows a circle with center O. P is mid-point of chord AB.

Show that OP is perpendicular to AB.
A line segment AB is bisected at point P and through point P another line segment PQ, which is perpendicular to AB, is drawn. Show that: QA = QB.
In ∆ABC, AB = AC. Show that the altitude AD is median also.
In the following diagram, ABCD is a square and APB is an equilateral triangle.
(i) Prove that: ΔAPD ≅ ΔBPC
(ii) Find the angles of ΔDPC.
In the following diagram, AP and BQ are equal and parallel to each other. 
Prove that: AB and PQ bisect each other.
In ΔABC, AB = AC and the bisectors of angles B and C intersect at point O.
Prove that : (i) BO = CO
(ii) AO bisects angle BAC.
In the following figure, ABC is an equilateral triangle in which QP is parallel to AC. Side AC is produced up to point R so that CR = BP.
Prove that QR bisects PC.
Hint: ( Show that ∆ QBP is equilateral
⇒ BP = PQ, but BP = CR
⇒ PQ = CR ⇒ ∆ QPM ≅ ∆ RCM ).
