Advertisements
Advertisements
Question
A line segment AB is bisected at point P and through point P another line segment PQ, which is perpendicular to AB, is drawn. Show that: QA = QB.
Solution
Given: A ΔABQ in which AB is bisected at P
PQ is perpendicular to AB
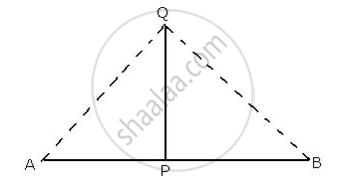
We need to prove that
QA = QB
Proof:
In ΔAPQ and ΔBPQ
AP = PB ...[ P is the mid-point of AB ]
∠QPA = ∠QPB = 90° ...[ PQ is perpendicular to AB ]
PQ = PQ ...[ Common]
∴ By Side-Angel-Side criterion of congruence,
ΔQAP ≅ ΔQBP
The corresponding parts of the congruent triangles are
congruent.
∴ QA = QB ...[ c.p.c.t ]
APPEARS IN
RELATED QUESTIONS
In quadrilateral ACBD, AC = AD and AB bisects ∠A (See the given figure). Show that ΔABC ≅ ΔABD. What can you say about BC and BD?

ABCD is a square, X and Yare points on sides AD and BC respectively such that AY = BX. Prove that BY = AX and ∠BAY = ∠ABX.
In two triangles ABC and ADC, if AB = AD and BC = CD. Are they congruent?
Use the information in the given figure to prove:
- AB = FE
- BD = CF

If the following pair of the triangle is congruent? state the condition of congruency:
In ΔABC and ΔPQR, AB = PQ, AC = PR, and BC = QR.
A triangle ABC has ∠B = ∠C.
Prove that: The perpendiculars from the mid-point of BC to AB and AC are equal.
A triangle ABC has ∠B = ∠C.
Prove that: The perpendiculars from B and C to the opposite sides are equal.
If AP bisects angle BAC and M is any point on AP, prove that the perpendiculars drawn from M to AB and AC are equal.
ABCD is a parallelogram. The sides AB and AD are produced to E and F respectively, such produced to E and F respectively, such that AB = BE and AD = DF.
Prove that: ΔBEC ≅ ΔDCF.
In a ΔABC, BD is the median to the side AC, BD is produced to E such that BD = DE.
Prove that: AE is parallel to BC.
