Advertisements
Advertisements
Question
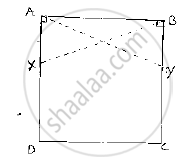
ABCD is a square, X and Yare points on sides AD and BC respectively such that AY = BX. Prove that BY = AX and ∠BAY = ∠ABX.
Solution
Given that ABCD is a square, X and Y are points on sides AD and BC respectively such that AY = BX.
We have to prove BY = AX and ∠BAY = ∠ABX
Join B and X, A and Y.
Since, ABCD is a square ⇒ ∠ DAB = ∠CBA =90°
⇒ ∠XAB= ∠YBA=90° .............(1)
Now, consider triangle XAB and YBA
We have
∠XAB=∠YBA=90° ...........[From (1)]
BX=AY [given]
And AB=BA [Common side]
So, by RHS congruence criterion, we have ΔXAB≅ΔYBA
Now, we know that corresponding parts of congruent triangles are equal.
∴ BY=AX and ∠BAY=∠ABX
∴ Hence proved
APPEARS IN
RELATED QUESTIONS
In the given figure, AC = AE, AB = AD and ∠BAD = ∠EAC. Show that BC = DE.

Which congruence criterion do you use in the following?
Given: AC = DF
AB = DE
BC = EF
So, ΔABC ≅ ΔDEF
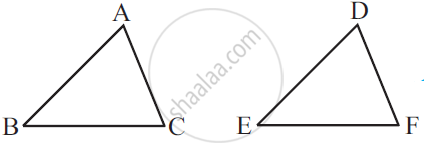
In ΔABC, ∠A = 30°, ∠B = 40° and ∠C = 110°
In ΔPQR, ∠P = 30°, ∠Q = 40° and ∠R = 110°
A student says that ΔABC ≅ ΔPQR by AAA congruence criterion. Is he justified? Why or why not?
In the given figure, prove that:
CD + DA + AB + BC > 2AC

In two triangles ABC and DEF, it is given that ∠A = ∠D, ∠B = ∠E and ∠C =∠F. Are the two triangles necessarily congruent?
If ABC and DEF are two triangles such that AC = 2.5 cm, BC = 5 cm, ∠C = 75°, DE = 2.5 cm, DF = 5cm and ∠D = 75°. Are two triangles congruent?
A triangle ABC has ∠B = ∠C.
Prove that: The perpendiculars from the mid-point of BC to AB and AC are equal.
A line segment AB is bisected at point P and through point P another line segment PQ, which is perpendicular to AB, is drawn. Show that: QA = QB.
In the following figure, OA = OC and AB = BC.
Prove that: ΔAOD≅ ΔCOD
ABC is a right triangle with AB = AC. Bisector of ∠A meets BC at D. Prove that BC = 2AD.
