Advertisements
Advertisements
Question
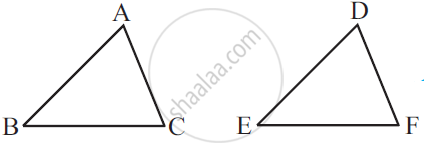
Which congruence criterion do you use in the following?
Given: AC = DF
AB = DE
BC = EF
So, ΔABC ≅ ΔDEF
Solution
SSS, as the sides of ΔABC are equal to the sides of ΔDEF.
APPEARS IN
RELATED QUESTIONS
Line l is the bisector of an angle ∠A and B is any point on l. BP and BQ are perpendiculars from B to the arms of ∠A (see the given figure). Show that:
- ΔAPB ≅ ΔAQB
- BP = BQ or B is equidistant from the arms of ∠A.
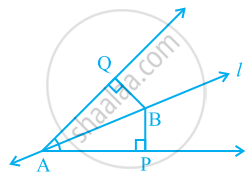
You have to show that ΔAMP ≅ AMQ.
In the following proof, supply the missing reasons.
| Steps | Reasons | ||
| 1 | PM = QM | 1 | ... |
| 2 | ∠PMA = ∠QMA | 2 | ... |
| 3 | AM = AM | 3 | ... |
| 4 | ΔAMP ≅ ΔAMQ | 4 | ... |

In ΔABC, ∠A = 30°, ∠B = 40° and ∠C = 110°
In ΔPQR, ∠P = 30°, ∠Q = 40° and ∠R = 110°
A student says that ΔABC ≅ ΔPQR by AAA congruence criterion. Is he justified? Why or why not?
If perpendiculars from any point within an angle on its arms are congruent, prove that it lies on the bisector of that angle.
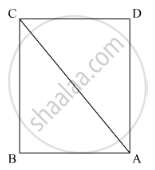
In the given figure, prove that:
CD + DA + AB > BC
In two triangles ABC and DEF, it is given that ∠A = ∠D, ∠B = ∠E and ∠C =∠F. Are the two triangles necessarily congruent?
If the following pair of the triangle is congruent? state the condition of congruency:
In ΔABC and ΔQRP, AB = QR, ∠B = ∠R and ∠C = P.
The following figure shows a circle with center O.

If OP is perpendicular to AB, prove that AP = BP.
In a triangle ABC, D is mid-point of BC; AD is produced up to E so that DE = AD.
Prove that :
(i) ΔABD and ΔECD are congruent.
(ii) AB = CE.
(iii) AB is parallel to EC
In ΔABC, AB = AC and the bisectors of angles B and C intersect at point O.
Prove that : (i) BO = CO
(ii) AO bisects angle BAC.
