Advertisements
Advertisements
Question
In a triangle ABC, D is mid-point of BC; AD is produced up to E so that DE = AD.
Prove that :
(i) ΔABD and ΔECD are congruent.
(ii) AB = CE.
(iii) AB is parallel to EC
Solution
Given: A ΔABC in which D is the mid-point of BC
AD is produced to E so that DE=AD
We need to prove that :
(i) ΔABD and ΔECD are congruent.
(ii) AB = CE.
(iii) AB is parallel to EC
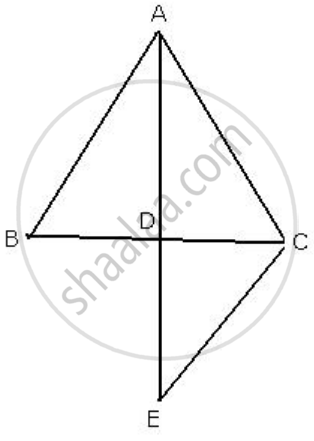
(i) In ΔABD and ΔECD
BD = DC ...[ D is the midpoint of BC ]
∠ADB =∠CDE ...[ vertically opposite angles ]
AD = DE ...[ Given ]
∴ By Side-Angle-Side criterion of congruence, we have,
ΔABD ≅ ΔECD
(ii) The corresponding parts of the congruent triangles are congruent.
∴ AB = EC ...[ c.p.c.t .c]
(iii) Also, ∠BAD = ∠DEC ....[ c.p.c t.c ]
∠ABD = ∠DCE .....[ c.p.c t.c ]
AB || EC .....[ DAB and DEC are alternate angles ]
APPEARS IN
RELATED QUESTIONS
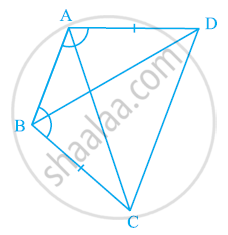
ABCD is a quadrilateral in which AD = BC and ∠DAB = ∠CBA (See the given figure). Prove that
- ΔABD ≅ ΔBAC
- BD = AC
- ∠ABD = ∠BAC.
In two triangles ABC and ADC, if AB = AD and BC = CD. Are they congruent?
In the given figure, ABC is an isosceles triangle whose side AC is produced to E. Through C, CD is drawn parallel to BA. The value of x is

In a triangle ABC, D is mid-point of BC; AD is produced up to E so that DE = AD. Prove that:
AB = CE.
A triangle ABC has ∠B = ∠C.
Prove that: The perpendiculars from the mid-point of BC to AB and AC are equal.
A triangle ABC has ∠B = ∠C.
Prove that: The perpendiculars from B and C to the opposite sides are equal.
The perpendicular bisectors of the sides of a triangle ABC meet at I.
Prove that: IA = IB = IC.
If AP bisects angle BAC and M is any point on AP, prove that the perpendiculars drawn from M to AB and AC are equal.
From the given diagram, in which ABCD is a parallelogram, ABL is a line segment and E is mid-point of BC.
Prove that:
(i) ΔDCE ≅ ΔLBE
(ii) AB = BL.
(iii) AL = 2DC
In a ΔABC, BD is the median to the side AC, BD is produced to E such that BD = DE.
Prove that: AE is parallel to BC.
