Advertisements
Advertisements
Question
If AP bisects angle BAC and M is any point on AP, prove that the perpendiculars drawn from M to AB and AC are equal.
Solution
From M, draw ML such that ML is perpendicular to AB and MN is perpendicular to AC
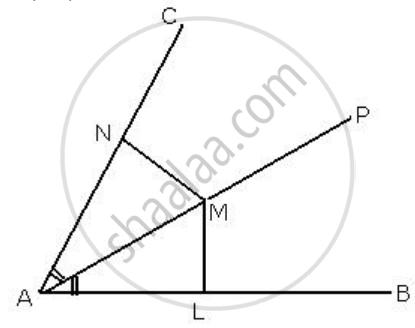
In ΔALM and ΔANM
∠LAM = ∠MAN ...[∵ AP is the bisector of BAC]
∠ALM = ∠ANM = 90° ...[∵ ML ⊥ AB, MN ⊥ AC]
AM = AM ...[Common]
∴ By angle-angle-Side criterion of congruence,
ΔALM ≅ ΔANM
The corresponding parts of the congruent triangles are congruent.
∴ ML = MN ...[c. p. c. t]
Hence, proved.
APPEARS IN
RELATED QUESTIONS
l and m are two parallel lines intersected by another pair of parallel lines p and q (see the given figure). Show that ΔABC ≅ ΔCDA.

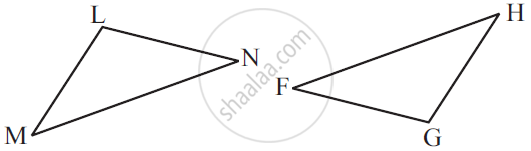
Which congruence criterion do you use in the following?
Given: ∠MLN = ∠FGH
∠NML = ∠GFH
ML = FG
So, ΔLMN ≅ ΔGFH
You want to show that ΔART ≅ ΔPEN,
If it is given that ∠T = ∠N and you are to use SAS criterion, you need to have
1) RT = and
2) PN =

Prove that the perimeter of a triangle is greater than the sum of its altitudes.
In the given figure, ABC is an isosceles triangle whose side AC is produced to E. Through C, CD is drawn parallel to BA. The value of x is

In a triangle ABC, D is mid-point of BC; AD is produced up to E so that DE = AD.
Prove that :
(i) ΔABD and ΔECD are congruent.
(ii) AB = CE.
(iii) AB is parallel to EC
A triangle ABC has ∠B = ∠C.
Prove that: The perpendiculars from the mid-point of BC to AB and AC are equal.
From the given diagram, in which ABCD is a parallelogram, ABL is a line segment and E is mid-point of BC.
Prove that:
(i) ΔDCE ≅ ΔLBE
(ii) AB = BL.
(iii) AL = 2DC
In ΔABC, AB = AC and the bisectors of angles B and C intersect at point O.
Prove that : (i) BO = CO
(ii) AO bisects angle BAC.
In a triangle, ABC, AB = BC, AD is perpendicular to side BC and CE is perpendicular to side AB.
Prove that: AD = CE.
