Advertisements
Advertisements
प्रश्न
If AP bisects angle BAC and M is any point on AP, prove that the perpendiculars drawn from M to AB and AC are equal.
उत्तर
From M, draw ML such that ML is perpendicular to AB and MN is perpendicular to AC
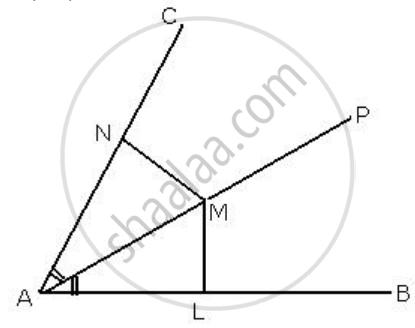
In ΔALM and ΔANM
∠LAM = ∠MAN ...[∵ AP is the bisector of BAC]
∠ALM = ∠ANM = 90° ...[∵ ML ⊥ AB, MN ⊥ AC]
AM = AM ...[Common]
∴ By angle-angle-Side criterion of congruence,
ΔALM ≅ ΔANM
The corresponding parts of the congruent triangles are congruent.
∴ ML = MN ...[c. p. c. t]
Hence, proved.
APPEARS IN
संबंधित प्रश्न
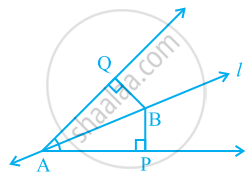
Line l is the bisector of an angle ∠A and B is any point on l. BP and BQ are perpendiculars from B to the arms of ∠A (see the given figure). Show that:
- ΔAPB ≅ ΔAQB
- BP = BQ or B is equidistant from the arms of ∠A.
ABCD is a square, X and Yare points on sides AD and BC respectively such that AY = BX. Prove that BY = AX and ∠BAY = ∠ABX.
ABC is an isosceles triangle in which AB = AC. BE and CF are its two medians. Show that BE = CF.
A triangle ABC has ∠B = ∠C.
Prove that: The perpendiculars from B and C to the opposite sides are equal.
In the given figure: AB//FD, AC//GE and BD = CE;
prove that:
- BG = DF
- CF = EG

In ∆ABC, AB = AC. Show that the altitude AD is median also.
A point O is taken inside a rhombus ABCD such that its distance from the vertices B and D are equal. Show that AOC is a straight line.
In the following figure, AB = EF, BC = DE and ∠B = ∠E = 90°.
Prove that AD = FC.
In the following figure, ∠A = ∠C and AB = BC.
Prove that ΔABD ≅ ΔCBE. 
Which of the following is not a criterion for congruence of triangles?
