Advertisements
Advertisements
प्रश्न
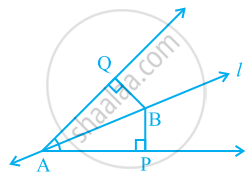
Line l is the bisector of an angle ∠A and B is any point on l. BP and BQ are perpendiculars from B to the arms of ∠A (see the given figure). Show that:
- ΔAPB ≅ ΔAQB
- BP = BQ or B is equidistant from the arms of ∠A.
उत्तर
We have, l is the bisector of ∠QAP.
∴ ∠QAB = ∠PAB
and ∠Q = ∠P ...[Each 90°]
⇒ ∠ABQ = ∠ABP ...[By angle sum property of △]
i. Now, in △APB and △AQB, we have
∠ABP = ∠ABQ ...[Proved above]
AB = BA ...[Common]
∠PAB ≅ ∠QAB ...[Given]
△APB ≅ △AQB ...[By ASA congruency]
ii. Since, △APB ≅ △AQB
⇒ BP = BQ ...[By Corresponding parts of congruent triangles]
i.e., [Perpendicular distance of B from AP] = [Perpendicular distance of B from AQ]
Thus, the point B is equidistant from the arms of ∠A.
APPEARS IN
संबंधित प्रश्न
AD and BC are equal perpendiculars to a line segment AB (See the given figure). Show that CD bisects AB.

l and m are two parallel lines intersected by another pair of parallel lines p and q (see the given figure). Show that ΔABC ≅ ΔCDA.

Which congruence criterion do you use in the following?
Given: AC = DF
AB = DE
BC = EF
So, ΔABC ≅ ΔDEF
If ΔABC and ΔPQR are to be congruent, name one additional pair of corresponding parts. What criterion did you use?
Which of the following statements are true (T) and which are false (F):
If any two sides of a right triangle are respectively equal to two sides of other right triangle, then the two triangles are congruent.
In Δ ABC, ∠B = 35°, ∠C = 65° and the bisector of ∠BAC meets BC in P. Arrange AP, BP and CP in descending order.
In two triangles ABC and DEF, it is given that ∠A = ∠D, ∠B = ∠E and ∠C =∠F. Are the two triangles necessarily congruent?
In triangles ABC and CDE, if AC = CE, BC = CD, ∠A = 60°, ∠C = 30° and ∠D = 90°. Are two triangles congruent?
The given figure shows a circle with center O. P is mid-point of chord AB.

Show that OP is perpendicular to AB.
In a ΔABC, BD is the median to the side AC, BD is produced to E such that BD = DE.
Prove that: AE is parallel to BC.
