Advertisements
Advertisements
प्रश्न
In the given figure, AC = AE, AB = AD and ∠BAD = ∠EAC. Show that BC = DE.

उत्तर
Given that
∠BAD = ∠EAC
On adding ∠DAC on both sides, we get
∠BAD + ∠DAC = ∠EAC + ∠DAC
⇒ ∠BAC = ∠EAD …(I)
Now, in △ABC and △AED,
AB = AD ...[Given]
AC = AE ...[Given]
∠BAC = ∠EAD ...[By (I)]
∴ △ABC ≌ △ADE ...[By AAS congruence rule]
⇒ BC = DE ...[Corresponding parts of congruent triangles]
APPEARS IN
संबंधित प्रश्न
You want to show that ΔART ≅ ΔPEN,
If you have to use SSS criterion, then you need to show
1) AR =
2) RT =
3) AT =

If ΔABC and ΔPQR are to be congruent, name one additional pair of corresponding parts. What criterion did you use?
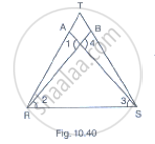
In Fig. 10.40, it is given that RT = TS, ∠1 = 2∠2 and ∠4 = 2∠3. Prove that ΔRBT ≅ ΔSAT.
In two triangles ABC and DEF, it is given that ∠A = ∠D, ∠B = ∠E and ∠C =∠F. Are the two triangles necessarily congruent?
D, E, F are the mid-point of the sides BC, CA and AB respectively of ΔABC. Then ΔDEF is congruent to triangle
In a triangle ABC, D is mid-point of BC; AD is produced up to E so that DE = AD.
Prove that :
(i) ΔABD and ΔECD are congruent.
(ii) AB = CE.
(iii) AB is parallel to EC
The perpendicular bisectors of the sides of a triangle ABC meet at I.
Prove that: IA = IB = IC.
In ∆ABC, AB = AC. Show that the altitude AD is median also.
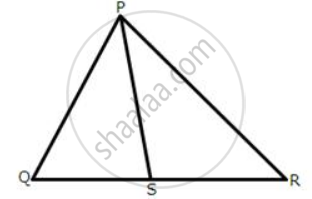
In the following figures, the sides AB and BC and the median AD of triangle ABC are equal to the sides PQ and QR and median PS of the triangle PQR.
Prove that ΔABC and ΔPQR are congruent.
 |
 |
In quadrilateral ABCD, AD = BC and BD = CA.
Prove that:
(i) ∠ADB = ∠BCA
(ii) ∠DAB = ∠CBA
