Advertisements
Advertisements
प्रश्न
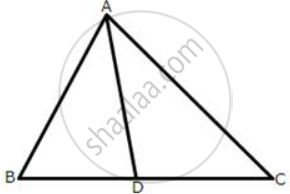
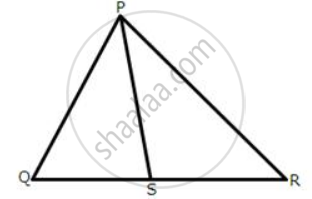
In the following figures, the sides AB and BC and the median AD of triangle ABC are equal to the sides PQ and QR and median PS of the triangle PQR.
Prove that ΔABC and ΔPQR are congruent.
 |
 |
उत्तर
Given: AB = PQ ; BC = QR ; AD = PS
To prove: ΔABC ≅ ΔPQR
Proof:
BC = QR
2 BD = 2 QS
BD = QS ...(i)
In Δ ABD and Δ PQS
AB = PQ ...[Given]
BD = QS ...[From equation (i)]
AD = PS ...[Given]
∴ ΔABD ≅ ΔPQS ...[by SSS rule]
Then, ∠B = ∠Q ...[by CPCTC] ...(ii)
In ΔABC and ΔPQR
AB = PQ ...[Given]
∠B = ∠Q ...[ii]
BC = QR ...[Given]
∴ ΔABC ≅ ΔPQR ...[by SAS rule]
Hence proved.
APPEARS IN
संबंधित प्रश्न
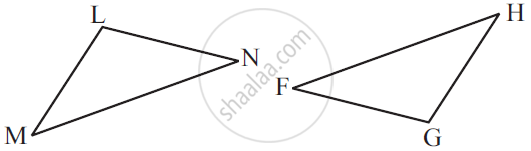
Which congruence criterion do you use in the following?
Given: ∠MLN = ∠FGH
∠NML = ∠GFH
ML = FG
So, ΔLMN ≅ ΔGFH
If perpendiculars from any point within an angle on its arms are congruent, prove that it lies on the bisector of that angle.
In Δ ABC, ∠B = 35°, ∠C = 65° and the bisector of ∠BAC meets BC in P. Arrange AP, BP and CP in descending order.
In two triangles ABC and DEF, it is given that ∠A = ∠D, ∠B = ∠E and ∠C =∠F. Are the two triangles necessarily congruent?
If the following pair of the triangle is congruent? state the condition of congruency :
In Δ ABC and Δ DEF, AB = DE, BC = EF and ∠ B = ∠ E.
The following figure shows a circle with center O.

If OP is perpendicular to AB, prove that AP = BP.
A triangle ABC has ∠B = ∠C.
Prove that: The perpendiculars from the mid-point of BC to AB and AC are equal.
If AP bisects angle BAC and M is any point on AP, prove that the perpendiculars drawn from M to AB and AC are equal.
From the given diagram, in which ABCD is a parallelogram, ABL is a line segment and E is mid-point of BC.
prove that : AL = 2DC
In ΔABC, AB = AC and the bisectors of angles B and C intersect at point O.
Prove that : (i) BO = CO
(ii) AO bisects angle BAC.
