Advertisements
Advertisements
प्रश्न
If the following pair of the triangle is congruent? state the condition of congruency :
In Δ ABC and Δ DEF, AB = DE, BC = EF and ∠ B = ∠ E.
उत्तर
In Δ ABC and Δ DEF,
AB = DE ...[ Given ]
∠B = ∠E ...[ Given ]
BC = EF ...[ Given ]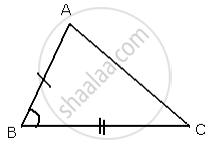
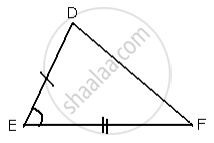
By Side - Angle - Side criterion of congruency, the triangles
Δ ABC and Δ DEF are congruent to each other.
∴ Δ ABC ≅ Δ DEF
APPEARS IN
संबंधित प्रश्न
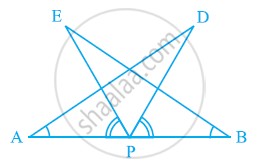
AB is a line segment and P is its mid-point. D and E are points on the same side of AB such that ∠BAD = ∠ABE and ∠EPA = ∠DPB (See the given figure). Show that
- ΔDAP ≅ ΔEBP
- AD = BE
You want to show that ΔART ≅ ΔPEN,
If it is given that ∠T = ∠N and you are to use SAS criterion, you need to have
1) RT = and
2) PN =

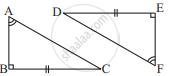
Explain, why ΔABC ≅ ΔFED.
In Δ ABC, ∠B = 35°, ∠C = 65° and the bisector of ∠BAC meets BC in P. Arrange AP, BP and CP in descending order.
In the given figure, prove that:
CD + DA + AB + BC > 2AC

In two congruent triangles ABC and DEF, if AB = DE and BC = EF. Name the pairs of equal angles.
ABC is an isosceles triangle in which AB = AC. BE and CF are its two medians. Show that BE = CF.
The following figure shows a circle with center O.

If OP is perpendicular to AB, prove that AP = BP.
In the figure, given below, triangle ABC is right-angled at B. ABPQ and ACRS are squares. 
Prove that:
(i) ΔACQ and ΔASB are congruent.
(ii) CQ = BS.
In a triangle, ABC, AB = BC, AD is perpendicular to side BC and CE is perpendicular to side AB.
Prove that: AD = CE.
