Advertisements
Advertisements
प्रश्न
Explain, why ΔABC ≅ ΔFED.
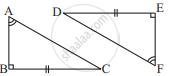
उत्तर
Given that, ∠ABC = ∠FED (1)
∠BAC = ∠EFD (2)
The two angles of ΔABC are equal to the two respective angles of ΔFED. Also, the sum of all interior angles of a triangle is 180º. Therefore, third angle of both triangles will also be equal in measure.
∠BCA = ∠EDF (3)
Also, given that, BC = ED (4)
By using equation (1), (3), and (4), we obtain
ΔABC ≅ ΔFED (ASA criterion)
APPEARS IN
संबंधित प्रश्न
In quadrilateral ACBD, AC = AD and AB bisects ∠A (See the given figure). Show that ΔABC ≅ ΔABD. What can you say about BC and BD?

In the given figure, AC = AE, AB = AD and ∠BAD = ∠EAC. Show that BC = DE.

Which congruence criterion do you use in the following?
Given: ZX = RP
RQ = ZY
∠PRQ = ∠XZY
So, ΔPQR ≅ ΔXYZ

Which of the following statements are true (T) and which are false (F):
If any two sides of a right triangle are respectively equal to two sides of other right triangle, then the two triangles are congruent.
In triangles ABC and CDE, if AC = CE, BC = CD, ∠A = 60°, ∠C = 30° and ∠D = 90°. Are two triangles congruent?
ABC is an isosceles triangle in which AB = AC. BE and CF are its two medians. Show that BE = CF.
If the following pair of the triangle is congruent? state the condition of congruency :
In Δ ABC and Δ DEF, AB = DE, BC = EF and ∠ B = ∠ E.
Use the information in the given figure to prove:
- AB = FE
- BD = CF

In a triangle ABC, D is mid-point of BC; AD is produced up to E so that DE = AD. Prove that:
AB = CE.
In the following diagram, AP and BQ are equal and parallel to each other. 
Prove that: AB and PQ bisect each other.
