Advertisements
Advertisements
प्रश्न
In triangles ABC and CDE, if AC = CE, BC = CD, ∠A = 60°, ∠C = 30° and ∠D = 90°. Are two triangles congruent?
उत्तर
For the triangles ABC and ECD, we have the following information and corresponding figure:
AC = CE
BC = CD
∠A = 60°
∠C = 30°
∠D = 90°
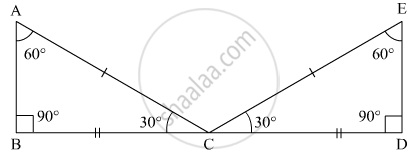
In triangles ABC and ECD, we have
AC = EC
BC = CD
and ∠BAC= ∠CED
The SSA criteria for two triangles to be congruent are being followed. So both the triangles are congruent.
APPEARS IN
संबंधित प्रश्न
In quadrilateral ACBD, AC = AD and AB bisects ∠A (See the given figure). Show that ΔABC ≅ ΔABD. What can you say about BC and BD?

Which congruence criterion do you use in the following?
Given: AC = DF
AB = DE
BC = EF
So, ΔABC ≅ ΔDEF
In the figure, the two triangles are congruent.
The corresponding parts are marked. We can write ΔRAT ≅ ?
In two congruent triangles ABC and DEF, if AB = DE and BC = EF. Name the pairs of equal angles.
In a triangle ABC, D is mid-point of BC; AD is produced up to E so that DE = AD. Prove that:
AB is parallel to EC.
In a ΔABC, BD is the median to the side AC, BD is produced to E such that BD = DE.
Prove that: AE is parallel to BC.
In the following figure, OA = OC and AB = BC.
Prove that: ΔAOD≅ ΔCOD
In the following figure, AB = EF, BC = DE and ∠B = ∠E = 90°.
Prove that AD = FC.
In ΔABC, AB = AC and the bisectors of angles B and C intersect at point O.
Prove that : (i) BO = CO
(ii) AO bisects angle BAC.
Which of the following is not a criterion for congruence of triangles?
