Advertisements
Advertisements
प्रश्न
Which of the following is not a criterion for congruence of triangles?
विकल्प
SAS
ASA
SSA
SSS
उत्तर
SSA
Explanation:
We know that,
Two triangles are congruent, if the side (S) and angles (A) of one triangle is equal to another.
And criterion for congruence of triangle are SAS, ASA, SSS and RHS.
SSA is not a criterion for congruence of triangles.
APPEARS IN
संबंधित प्रश्न
In quadrilateral ACBD, AC = AD and AB bisects ∠A (See the given figure). Show that ΔABC ≅ ΔABD. What can you say about BC and BD?

In ΔABC, ∠A = 30°, ∠B = 40° and ∠C = 110°
In ΔPQR, ∠P = 30°, ∠Q = 40° and ∠R = 110°
A student says that ΔABC ≅ ΔPQR by AAA congruence criterion. Is he justified? Why or why not?
If ΔABC and ΔPQR are to be congruent, name one additional pair of corresponding parts. What criterion did you use?
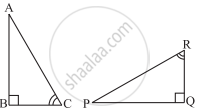
In the given figure, ABC is an isosceles triangle whose side AC is produced to E. Through C, CD is drawn parallel to BA. The value of x is

If the following pair of the triangle is congruent? state the condition of congruency:
In ΔABC and ΔQRP, AB = QR, ∠B = ∠R and ∠C = P.
From the given diagram, in which ABCD is a parallelogram, ABL is a line segment and E is mid-point of BC.
prove that : AL = 2DC
In the following figure, AB = AC and AD is perpendicular to BC. BE bisects angle B and EF is perpendicular to AB.
Prove that : ED = EF

In quadrilateral ABCD, AD = BC and BD = CA.
Prove that:
(i) ∠ADB = ∠BCA
(ii) ∠DAB = ∠CBA
AD and BC are equal perpendiculars to a line segment AB. If AD and BC are on different sides of AB prove that CD bisects AB.
ABC is an isosceles triangle with AB = AC and BD and CE are its two medians. Show that BD = CE.
