Advertisements
Advertisements
प्रश्न
In the following figure, AB = AC and AD is perpendicular to BC. BE bisects angle B and EF is perpendicular to AB.
Prove that : ED = EF

उत्तर
In ΔEFB and ΔEDB,
∠EFB = ∠EDB ( both are 900 )
EB = EB ( common side )
∠FBE = ∠DBE ( given )
ΔEFB ≅ ΔEDB (AAS congruence criterion)
⇒ EF = ED (cpct )
that is , Ed = EF.
APPEARS IN
संबंधित प्रश्न
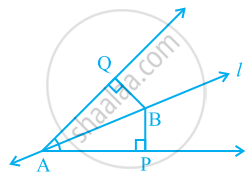
Line l is the bisector of an angle ∠A and B is any point on l. BP and BQ are perpendiculars from B to the arms of ∠A (see the given figure). Show that:
- ΔAPB ≅ ΔAQB
- BP = BQ or B is equidistant from the arms of ∠A.
Which congruence criterion do you use in the following?
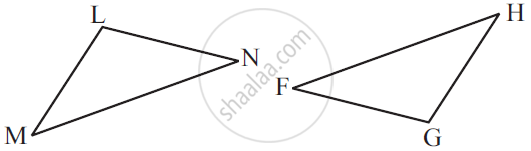
Given: ∠MLN = ∠FGH
∠NML = ∠GFH
ML = FG
So, ΔLMN ≅ ΔGFH
If ΔABC and ΔPQR are to be congruent, name one additional pair of corresponding parts. What criterion did you use?
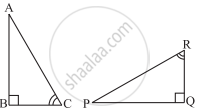
In Fig. 10.99, AD ⊥ CD and CB ⊥. CD. If AQ = BP and DP = CQ, prove that ∠DAQ = ∠CBP.

In the given figure, ABC is an isosceles triangle whose side AC is produced to E. Through C, CD is drawn parallel to BA. The value of x is

From the given diagram, in which ABCD is a parallelogram, ABL is a line segment and E is mid-point of BC.
Prove that: AB = BL.
In the following figure, BL = CM.

Prove that AD is a median of triangle ABC.
In the following diagram, ABCD is a square and APB is an equilateral triangle.
(i) Prove that: ΔAPD ≅ ΔBPC
(ii) Find the angles of ΔDPC.
PQRS is a parallelogram. L and M are points on PQ and SR respectively such that PL = MR.
Show that LM and QS bisect each other.
Which of the following is not a criterion for congruence of triangles?
