Advertisements
Advertisements
प्रश्न
PQRS is a parallelogram. L and M are points on PQ and SR respectively such that PL = MR.
Show that LM and QS bisect each other.
उत्तर

Given: PL = MR ...(i)
To prove SR = PQ ...(ii) (parallelogram opposite sides)
SP - PQ and SR - MR
LQ = SM ...(iii)
In ΔLOQ & ΔMOS
∠LQO = ∠MSO ....( alternate interior angles )
∠OLQ = ∠OMS ....( alternate interior angles )
LQ = SM ...(from (iii))
ΔLOQ ≅ ∠MSO ...(by ASA congruence)
Then, OL = OM
OQ = OS ...(by c.p.c.t.c)
Hence, LM and QS bisect each other.
APPEARS IN
संबंधित प्रश्न
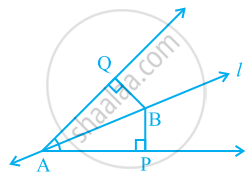
Line l is the bisector of an angle ∠A and B is any point on l. BP and BQ are perpendiculars from B to the arms of ∠A (see the given figure). Show that:
- ΔAPB ≅ ΔAQB
- BP = BQ or B is equidistant from the arms of ∠A.
Which congruence criterion do you use in the following?
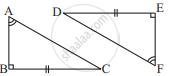
Given: EB = DB
AE = BC
∠A = ∠C = 90°
So, ΔABE ≅ ΔCDB

You have to show that ΔAMP ≅ AMQ.
In the following proof, supply the missing reasons.
| Steps | Reasons | ||
| 1 | PM = QM | 1 | ... |
| 2 | ∠PMA = ∠QMA | 2 | ... |
| 3 | AM = AM | 3 | ... |
| 4 | ΔAMP ≅ ΔAMQ | 4 | ... |

Explain, why ΔABC ≅ ΔFED.
If the following pair of the triangle is congruent? state the condition of congruency :
In Δ ABC and Δ DEF, AB = DE, BC = EF and ∠ B = ∠ E.
The following figure shows a circle with center O.

If OP is perpendicular to AB, prove that AP = BP.
In a triangle ABC, D is mid-point of BC; AD is produced up to E so that DE = AD. Prove that:
AB is parallel to EC.
A triangle ABC has ∠B = ∠C.
Prove that: The perpendiculars from the mid-point of BC to AB and AC are equal.
From the given diagram, in which ABCD is a parallelogram, ABL is a line segment and E is mid-point of BC.
Prove that:
(i) ΔDCE ≅ ΔLBE
(ii) AB = BL.
(iii) AL = 2DC
In ∆ABC, AB = AC. Show that the altitude AD is median also.
