Advertisements
Advertisements
प्रश्न
From the given diagram, in which ABCD is a parallelogram, ABL is a line segment and E is mid-point of BC.
Prove that:
(i) ΔDCE ≅ ΔLBE
(ii) AB = BL.
(iii) AL = 2DC
Advertisements
उत्तर
Given: ABCD is a parallelogram in which is the mid-point of BC.
We need to prove that
(i) ΔDCE ≅ ΔLBE
(ii) AB = BL.
(iii) AL = 2DC
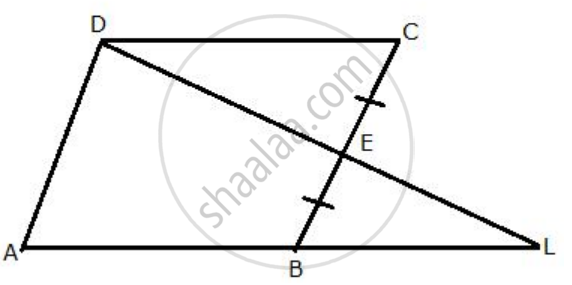
(i) In ΔDCE and ΔLBE
∠DCE = ∠EBL ...[DC || AB, alternate angels]
CE = EB ...[ E is the midpoint of BC]
∠DEC= ∠LEB ...[ vertically opposite angels]
∴ By Angel-SIde-Angel Criterion of congruence, we have,
ΔDCE ≅ ΔLBE
The corresponding parts of the congruent triangles are congruent.
∴ DC= LB ...[ c. p. c .t] ....(1)
(ii) DC= AB ...[ opposite sides of a parallelogram]...(2)
From ( 1 ) and ( 2 ), Ab = BL ...(3)
(iii) Al = AB+ BL ... (4)
From (3) and (4), Al = AB + AB
⇒AL = 2AB
⇒AL = 2DC ...[ From (2) ]
APPEARS IN
संबंधित प्रश्न
Which congruence criterion do you use in the following?
Given: ZX = RP
RQ = ZY
∠PRQ = ∠XZY
So, ΔPQR ≅ ΔXYZ
You want to show that ΔART ≅ ΔPEN,
If it is given that AT = PN and you are to use ASA criterion, you need to have
1) ?
2) ?
In Fig. 10.99, AD ⊥ CD and CB ⊥. CD. If AQ = BP and DP = CQ, prove that ∠DAQ = ∠CBP.
In two triangles ABC and ADC, if AB = AD and BC = CD. Are they congruent?
The following figure shows a circle with center O.
If OP is perpendicular to AB, prove that AP = BP.
In a triangle ABC, D is mid-point of BC; AD is produced up to E so that DE = AD. Prove that:
AB is parallel to EC.
In the following figure, AB = AC and AD is perpendicular to BC. BE bisects angle B and EF is perpendicular to AB.
Prove that : ED = EF
In the following figure, OA = OC and AB = BC.
Prove that: ΔAOD≅ ΔCOD
PQRS is a parallelogram. L and M are points on PQ and SR respectively such that PL = MR.
Show that LM and QS bisect each other.
ABC is an isosceles triangle with AB = AC and BD and CE are its two medians. Show that BD = CE.
