Advertisements
Advertisements
Question
From the given diagram, in which ABCD is a parallelogram, ABL is a line segment and E is mid-point of BC.
Prove that:
(i) ΔDCE ≅ ΔLBE
(ii) AB = BL.
(iii) AL = 2DC
Solution
Given: ABCD is a parallelogram in which is the mid-point of BC.
We need to prove that
(i) ΔDCE ≅ ΔLBE
(ii) AB = BL.
(iii) AL = 2DC
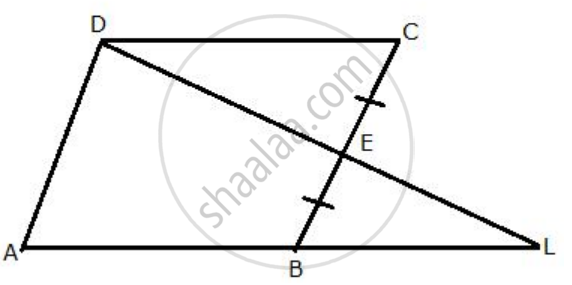
(i) In ΔDCE and ΔLBE
∠DCE = ∠EBL ...[DC || AB, alternate angels]
CE = EB ...[ E is the midpoint of BC]
∠DEC= ∠LEB ...[ vertically opposite angels]
∴ By Angel-SIde-Angel Criterion of congruence, we have,
ΔDCE ≅ ΔLBE
The corresponding parts of the congruent triangles are congruent.
∴ DC= LB ...[ c. p. c .t] ....(1)
(ii) DC= AB ...[ opposite sides of a parallelogram]...(2)
From ( 1 ) and ( 2 ), Ab = BL ...(3)
(iii) Al = AB+ BL ... (4)
From (3) and (4), Al = AB + AB
⇒AL = 2AB
⇒AL = 2DC ...[ From (2) ]
APPEARS IN
RELATED QUESTIONS
In quadrilateral ACBD, AC = AD and AB bisects ∠A (See the given figure). Show that ΔABC ≅ ΔABD. What can you say about BC and BD?

In right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see the given figure). Show that:
- ΔAMC ≅ ΔBMD
- ∠DBC is a right angle.
- ΔDBC ≅ ΔACB
- CM = `1/2` AB

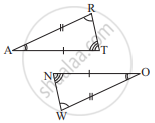
In the figure, the two triangles are congruent.
The corresponding parts are marked. We can write ΔRAT ≅ ?
Which of the following statements are true (T) and which are false (F):
Two right triangles are congruent if hypotenuse and a side of one triangle are respectively equal equal to the hypotenuse and a side of the other triangle.
In triangles ABC and CDE, if AC = CE, BC = CD, ∠A = 60°, ∠C = 30° and ∠D = 90°. Are two triangles congruent?
If the following pair of the triangle is congruent? state the condition of congruency :
In Δ ABC and Δ DEF, AB = DE, BC = EF and ∠ B = ∠ E.
Use the information in the given figure to prove:
- AB = FE
- BD = CF

The given figure shows a circle with center O. P is mid-point of chord AB.

Show that OP is perpendicular to AB.
From the given diagram, in which ABCD is a parallelogram, ABL is a line segment and E is mid-point of BC.
Prove that: AB = BL.
In the given figure: AB//FD, AC//GE and BD = CE;
prove that:
- BG = DF
- CF = EG

