Advertisements
Advertisements
Question
In right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see the given figure). Show that:
- ΔAMC ≅ ΔBMD
- ∠DBC is a right angle.
- ΔDBC ≅ ΔACB
- CM = `1/2` AB

Solution
Since M is the mid-point of AB.
∴ BM = AM
i. In ΔAMC and ΔBMD, we have
CM = DM ...[Given]
∠AMC = ∠BMD ...[Vertically opposite angles]
AM = BM ...[Proved above]
∴ ΔAMC ≅ ΔBMD ...[By SAS congruency]
ii. Since ΔAMC ≅ ΔBMD
∠MAC = ∠MBD ...[By corresponding parts of congruent triangles]
But they form a pair of alternate interior angles.
∴ AC ‖ DB
Now, BC is a transversal which intersects parallel lines AC and DB,
∴ ∠BCA + ∠DBC = 180° ...[Co-interior angles]
But ∠BCA = 90° ...[ΔABC is right angled at C]
∴ 90° + ∠DBC = 180°
⇒ ∠DBC = 90°
iii. Again, ΔAMC ≅ ΔBMD ...[Proved above]
∴ AC = BD ...[By corresponding parts of congruent triangles]
Now, in ΔDBC and ΔACB, we have
BD = CA ...[Proved above]
∠DBC = ∠ACB ...[Each 90°]
BC = CB ...[Common]
∴ ΔDBC ≅ ΔACB ...[By SAS congruency]
iv. As ΔDBC ≅ ΔACB
⇒ DC = AB ...[By corresponding parts of congruent triangles]
But DM = CM ...[Given]
∴ CM = `1/2` DC = `1/2` AB
⇒ CM = `1/2` AB.
APPEARS IN
RELATED QUESTIONS
Which congruence criterion do you use in the following?
Given: AC = DF
AB = DE
BC = EF
So, ΔABC ≅ ΔDEF
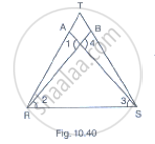
In Fig. 10.40, it is given that RT = TS, ∠1 = 2∠2 and ∠4 = 2∠3. Prove that ΔRBT ≅ ΔSAT.
If perpendiculars from any point within an angle on its arms are congruent, prove that it lies on the bisector of that angle.
Which of the following statements are true (T) and which are false (F):
Two right triangles are congruent if hypotenuse and a side of one triangle are respectively equal equal to the hypotenuse and a side of the other triangle.
In two triangles ABC and DEF, it is given that ∠A = ∠D, ∠B = ∠E and ∠C =∠F. Are the two triangles necessarily congruent?
If ABC and DEF are two triangles such that AC = 2.5 cm, BC = 5 cm, ∠C = 75°, DE = 2.5 cm, DF = 5cm and ∠D = 75°. Are two triangles congruent?
ABCD is a parallelogram. The sides AB and AD are produced to E and F respectively, such produced to E and F respectively, such that AB = BE and AD = DF.
Prove that: ΔBEC ≅ ΔDCF.
In a ΔABC, BD is the median to the side AC, BD is produced to E such that BD = DE.
Prove that: AE is parallel to BC.
In the figure, given below, triangle ABC is right-angled at B. ABPQ and ACRS are squares. 
Prove that:
(i) ΔACQ and ΔASB are congruent.
(ii) CQ = BS.
PQRS is a parallelogram. L and M are points on PQ and SR respectively such that PL = MR.
Show that LM and QS bisect each other.
