Advertisements
Advertisements
Question
In an isosceles triangle ABC, with AB = AC, the bisectors of ∠B and ∠C intersect each other at O. Join A to O. Show that:
- OB = OC
- AO bisects ∠A
Solution

(i) ABC is an isosceles triangle in which AB = AC
∠C = ∠B ...[Angles opposite to equal sides in a triangle are equal.]
⇒ ∠OCA + ∠OCB = ∠OBA + ∠OBC
⇒ ∠OCB + ∠OCB = ∠OBC + ∠OBC
∵ OB bisects ∠B.
∴ ∠OBA = ∠OBC
And OC bisects ∠C.
∴ ∠OCA = ∠OCB
⇒ 2∠OCB = 2∠OBC
⇒ ∠OCB = ∠OBC
Now, in △OBC,
∠OCB = ∠OBC ...[Proved above]
∴ OB = OC ...[Sides opposite to equal angles]
(ii) Now, in △AOB and △AOC,
AB = AC ...[Given]
∠OBA = ∠OCA
∠B = ∠C
BO bisects ∠B and CO bisects ∠C.
∠OBA = ∠OCA
OB = OC
∴ △AOB ≌ △AOC ...[By SAS congruence rule]
⇒ ∠OAB = ∠OAC ...[Corresponding parts of congruent triangles]
So, AO bisects ∠A.
APPEARS IN
RELATED QUESTIONS
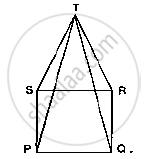
In Fig. 10.23, PQRS is a square and SRT is an equilateral triangle. Prove that
(i) PT = QT (ii) ∠TQR = 15°
In a ΔABC, if ∠A=l20° and AB = AC. Find ∠B and ∠C.
If the bisector of the exterior vertical angle of a triangle be parallel to the base. Show that the triangle is isosceles.
P is a point on the bisector of an angle ∠ABC. If the line through P parallel to AB meets BC at Q, prove that triangle BPQ is isosceles.
Which of the following statements are true (T) and which are false (F)?
Sum of the three sides of a triangle is less than the sum of its three altitudes.
Which of the following statements are true (T) and which are false (F)?
Sum of any two sides of a triangle is greater than the third side.
Fill in the blank to make the following statement true.
If two sides of a triangle are unequal, then the larger side has .... angle opposite to it.
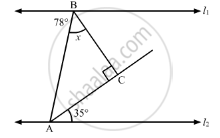
In the given figure, for which value of x is l1 || l2?
The side BC of ΔABC is produced to a point D. The bisector of ∠A meets side BC in L. If ∠ABC = 30° and ∠ACD = 115°, then ∠ALC = ______.
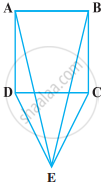
CDE is an equilateral triangle formed on a side CD of a square ABCD (Figure). Show that ∆ADE ≅ ∆BCE.