Advertisements
Advertisements
Question
The side BC of ΔABC is produced to a point D. The bisector of ∠A meets side BC in L. If ∠ABC = 30° and ∠ACD = 115°, then ∠ALC = ______.
Options
85°
- \[72\frac{1}{2}^\circ\]
145°
none of these
Solution
The side BC of ΔABC is produced to a point D. The bisector of ∠A meets side BC in L. If ∠ABC = 30° and ∠ACD = 115°, then ∠ALC = `bbunderline(72 1/2)` °
Explanation:
In the given problem, BC of ΔABC is produced to point D. bisectors of ∠A meet side BC at L, ∠ABC = 30° and ∠ACD = 115°
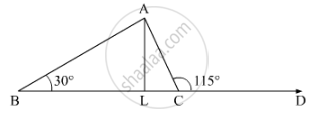
Here, using the property, “exterior angle of a triangle is equal to the sum of the two opposite interior angles”, we get,
In ΔABC
∠ACD = ∠CAB + ∠CBA
115° = ∠CAB + 30°
∠CAB = 115° - 30°
∠CAB = 85°
Now, as AL is the bisector of ∠A
∠CAL = 1/2 ∠CAB
∠CAL = 1/2 (85°)
`∠CAL = 44 (1^\circ)/2`
Also, ∠ACD is the exterior angle of ΔALC
Thus,
Again, using the property, “exterior angle of a triangle is equal to the sum of the two opposite interior angles”, we get,
In ΔALC
∠ACD = ∠CAL + ∠ALC
`115= 44 (1^\circ)/2+∠ALC`
`∠ALC =115- 44 1^\circ/2`
`∠ALC = 72 (1^\circ)/2`
Thus, `∠ALC = 72 1^\circ/2 `
APPEARS IN
RELATED QUESTIONS
ABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (see the given figure). Show that
- ΔABE ≅ ΔACF
- AB = AC, i.e., ABC is an isosceles triangle.

AB is a line seg P and Q are points on opposite sides of AB such that each of them is equidistant from the points A and B (See Fig. 10.26). Show that the line PQ is perpendicular bisector of AB.
The vertical angle of an isosceles triangle is 100°. Find its base angles.
Find the measure of each exterior angle of an equilateral triangle.
Angles A, B, C of a triangle ABC are equal to each other. Prove that ΔABC is equilateral.
Which of the following statements are true (T) and which are false (F):
If the bisector of the vertical angle of a triangle bisects the base, then the triangle may be isosceles.
Which of the following statements are true (T) and which are false (F)?
Sum of the three sides of a triangle is less than the sum of its three altitudes.
Which of the following statements are true (T) and which are false (F)?
Sum of any two sides of a triangle is greater than twice the median drawn to the third side.
Fill in the blank to make the following statement true.
If two angles of a triangle are unequal, then the smaller angle has the........ side opposite to it.
Is it possible to construct a triangle with lengths of its sides as 8 cm, 7 cm and 4 cm? Give reason for your answer.
