Advertisements
Advertisements
प्रश्न
The side BC of ΔABC is produced to a point D. The bisector of ∠A meets side BC in L. If ∠ABC = 30° and ∠ACD = 115°, then ∠ALC = ______.
विकल्प
85°
- \[72\frac{1}{2}^\circ\]
145°
none of these
Advertisements
उत्तर
The side BC of ΔABC is produced to a point D. The bisector of ∠A meets side BC in L. If ∠ABC = 30° and ∠ACD = 115°, then ∠ALC = `bbunderline(72 1/2)` °
Explanation:
In the given problem, BC of ΔABC is produced to point D. bisectors of ∠A meet side BC at L, ∠ABC = 30° and ∠ACD = 115°
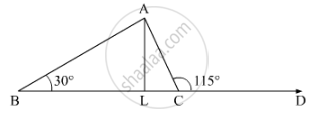
Here, using the property, “exterior angle of a triangle is equal to the sum of the two opposite interior angles”, we get,
In ΔABC
∠ACD = ∠CAB + ∠CBA
115° = ∠CAB + 30°
∠CAB = 115° - 30°
∠CAB = 85°
Now, as AL is the bisector of ∠A
∠CAL = 1/2 ∠CAB
∠CAL = 1/2 (85°)
`∠CAL = 44 (1^\circ)/2`
Also, ∠ACD is the exterior angle of ΔALC
Thus,
Again, using the property, “exterior angle of a triangle is equal to the sum of the two opposite interior angles”, we get,
In ΔALC
∠ACD = ∠CAL + ∠ALC
`115= 44 (1^\circ)/2+∠ALC`
`∠ALC =115- 44 1^\circ/2`
`∠ALC = 72 (1^\circ)/2`
Thus, `∠ALC = 72 1^\circ/2 `
APPEARS IN
संबंधित प्रश्न
In Figure AB = AC and ∠ACD =105°, find ∠BAC.
AB is a line seg P and Q are points on opposite sides of AB such that each of them is equidistant from the points A and B (See Fig. 10.26). Show that the line PQ is perpendicular bisector of AB.
In Fig. 10.23, PQRS is a square and SRT is an equilateral triangle. Prove that
(i) PT = QT (ii) ∠TQR = 15°
The vertical angle of an isosceles triangle is 100°. Find its base angles.
In a ΔABC, it is given that AB = AC and the bisectors of ∠B and ∠C intersect at O. If M is a point on BO produced, prove that ∠MOC = ∠ABC.
Which of the following statements are true (T) and which are false (F):
Sides opposite to equal angles of a triangle may be unequal
In a ΔABC, if ∠B = ∠C = 45°, which is the longest side?
In ΔABC, side AB is produced to D so that BD = BC. If ∠B = 60° and ∠A = 70°, prove that: (i) AD > CD (ii) AD > AC
Which of the following statements are true (T) and which are false (F)?
Sum of any two sides of a triangle is greater than twice the median drawn to the third side.
Which of the following statements are true (T) and which are false (F)?
Sum of any two sides of a triangle is greater than the third side.
Which of the following statements are true (T) and which are false (F)?
Difference of any two sides of a triangle is equal to the third side.
Which of the following statements are true (T) and which are false (F)?
Of all the line segments that can be drawn from a point to a line not containing it, the perpendicular line segment is the shortest one.
If the measures of angles of a triangle are in the ratio of 3 : 4 : 5, what is the measure of the smallest angle of the triangle?
In the given figure, if AB ⊥ BC. then x =
If the bisectors of the acute angles of a right triangle meet at O, then the angle at Obetween the two bisectors is
In a ΔABC, ∠A = 50° and BC is produced to a point D. If the bisectors of ∠ABC and ∠ACDmeet at E, then ∠E =
Two sides of a triangle are of lengths 5 cm and 1.5 cm. The length of the third side of the triangle cannot be ______.
In the following figure, D and E are points on side BC of a ∆ABC such that BD = CE and AD = AE. Show that ∆ABD ≅ ∆ACE.
