Advertisements
Advertisements
प्रश्न
In a ΔABC, ∠A = 50° and BC is produced to a point D. If the bisectors of ∠ABC and ∠ACDmeet at E, then ∠E =
विकल्प
25°
50°
100°
75°
उत्तर
In the given figure, bisectors of ∠ABCand ∠ACDmeet at E and ∠BAC = 50°
We need to find ∠BEC
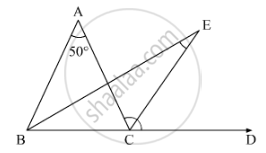
Here, using the property, “an exterior angle of the triangle is equal to the sum of the opposite interior angles”, we get,
In ΔABC with ∠ACD as its exterior angle
ext . ∠ACD = ∠A + ∠ABC ........(1)
Similarly, in Δ BECwith ∠ECDas its exterior angle
ext . ∠ECD = ∠EBC + ∠BEC
`1/2 ∠ACD = 1/2 ∠ABC + BEC`
(CE and BE are the bisectors of ∠ACD and ∠ABC)
∠BEC = 1/2 ∠ACD - 1/2 ∠ABC .......(2)
Now, multiplying both sides of (1) by 1/2
We get,
`1/2 ∠ACD = 1/2 ∠A +1/2 ∠ABC`
`1/2 ∠A = 1/2 ∠ACD - 1/2 ∠ABC` ......(3)
From (2) and (3) we get,
`∠BEC =1/2 ∠A`
`∠BEC =1/2 (50°)`
`∠BEC = 25°`
Thus, `∠BEC = 25°`
APPEARS IN
संबंधित प्रश्न
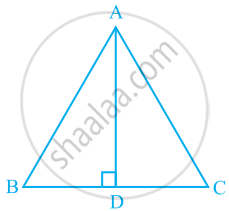
In ΔABC, AD is the perpendicular bisector of BC (see the given figure). Show that ΔABC is an isosceles triangle in which AB = AC.
P is a point on the bisector of an angle ∠ABC. If the line through P parallel to AB meets BC at Q, prove that triangle BPQ is isosceles.
ABC is a triangle in which ∠B = 2 ∠C. D is a point on BC such that AD bisects ∠BAC and AB = CD.
Prove that ∠BAC = 72°.
ABC is a right angled triangle in which ∠A = 90° and AB = AC. Find ∠B and ∠C.
Fill the blank in the following so that the following statement is true.
In a ΔABC if ∠A = ∠C , then AB = ......
Fill the blank in the following so that the following statement is true.
In right triangles ABC and DEF, if hypotenuse AB = EF and side AC = DE, then ΔABC ≅ Δ ……
Which of the following statements are true (T) and which are false (F)?
Sum of the three sides of a triangle is less than the sum of its three altitudes.
In a ΔABC, if ∠A = 60°, ∠B = 80° and the bisectors of ∠B and ∠C meet at O, then ∠BOC =
The base BC of triangle ABC is produced both ways and the measure of exterior angles formed are 94° and 126°. Then, ∠BAC =
The side BC of ΔABC is produced to a point D. The bisector of ∠A meets side BC in L. If ∠ABC = 30° and ∠ACD = 115°, then ∠ALC = ______.
