Advertisements
Advertisements
प्रश्न
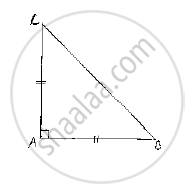
ABC is a right angled triangle in which ∠A = 90° and AB = AC. Find ∠B and ∠C.
उत्तर
Given that ABC is a right angled triangle such that ∠A = 90° and AB = AC Since,
AB = AC ⇒ ΔABC is also isosceles
∴ We can say that ΔABC is right angled isosceles triangle
⇒ ∠C=∠B and ∠A=90° ................(1)
Now, we have
Sum of angled in a triangle =180°
⇒ ∠A+∠B+∠C=180°
⇒ 90°+∠B+∠B=180° [∵ From (1)]
⇒ 2∠B=180°-90°
⇒`∠B=(90°)/2=45°`
∴ ∠B=∠C=45°
APPEARS IN
संबंधित प्रश्न
If the base of an isosceles triangle is produced on both sides, prove that the exterior angles so formed are equal to each other.
If the bisector of the exterior vertical angle of a triangle be parallel to the base. Show that the triangle is isosceles.
PQR is a triangle in which PQ = PR and S is any point on the side PQ. Through S, a line is drawn parallel to QR and intersecting PR at T. Prove that PS = PT.
ABC is a triangle and D is the mid-point of BC. The perpendiculars from D to AB and AC are equal. Prove that the triangle is isosceles.
In a triangle ABC, if AB = AC and AB is produced to D such that BD = BC, find ∠ACD: ∠ADC.
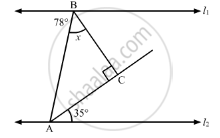
In the given figure, for which value of x is l1 || l2?
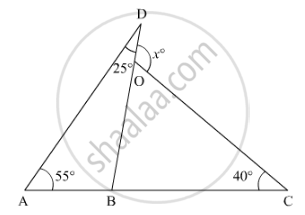
In the given figure, the value of x is ______.
In ∆ABC, BC = AB and ∠B = 80°. Then ∠A is equal to ______.
D is a point on the side BC of a ∆ABC such that AD bisects ∠BAC. Then ______.
In a triangle ABC, D is the mid-point of side AC such that BD = `1/2` AC. Show that ∠ABC is a right angle.
