Advertisements
Advertisements
प्रश्न
ABC is a triangle and D is the mid-point of BC. The perpendiculars from D to AB and AC are equal. Prove that the triangle is isosceles.
Advertisements
उत्तर
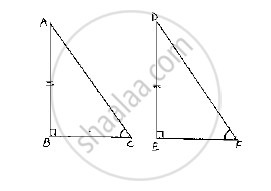
Given that, in two right triangles one side and acute angle of one are equal to the corresponding side and angle of the other
We have to prove that the triangles are congruent
Let us consider two right triangles such that
∠B=∠E=90° .................(1)
AB=DE ..................(2)
∠C=∠F ..................(3)
Now observe the two triangles ABC and DEF
∠C=∠F [From (3)]
∠B=∠E [From (4)]
and AB =DE [From (2)]
So, by AAS congruence criterion, we have
ΔABC≅ΔDEF
∴ The two triangles are congruent
Hence proved
APPEARS IN
संबंधित प्रश्न
ABC and DBC are two isosceles triangles on the same base BC (see the given figure). Show that ∠ABD = ∠ACD.
ΔABC is an isosceles triangle in which AB = AC. Side BA is produced to D such that AD = AB (see the given figure). Show that ∠BCD is a right angle.
In a ΔABC, if ∠A=l20° and AB = AC. Find ∠B and ∠C.
In Figure AB = AC and ∠ACD =105°, find ∠BAC.
In figure, AB = AC and DB = DC, find the ratio ∠ABD : ∠ACD
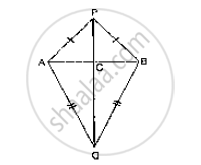
AB is a line seg P and Q are points on opposite sides of AB such that each of them is equidistant from the points A and B (See Fig. 10.26). Show that the line PQ is perpendicular bisector of AB.
In Fig. 10.23, PQRS is a square and SRT is an equilateral triangle. Prove that
(i) PT = QT (ii) ∠TQR = 15°
If the base of an isosceles triangle is produced on both sides, prove that the exterior angles so formed are equal to each other.
Which of the following statements are true (T) and which are false (F):
Angles opposite to equal sides of a triangle are equal
Which of the following statements are true (T) and which are false (F):
The measure of each angle of an equilateral triangle is 60°
Fill in the blank to make the following statement true.
In a right triangle the hypotenuse is the .... side.
In a ΔABC, if ∠A = 60°, ∠B = 80° and the bisectors of ∠B and ∠C meet at O, then ∠BOC =
Line segments AB and CD intersect at O such that AC || DB. If ∠CAB = 45° and ∠CDB = 55°, then ∠BOD =
In the given figure, for which value of x is l1 || l2?
In the given figure, AB and CD are parallel lines and transversal EF intersects them at Pand Q respectively. If ∠APR = 25°, ∠RQC = 30° and ∠CQF = 65°, then
The angles of a right angled triangle are
In ∆ABC, AB = AC and ∠B = 50°. Then ∠C is equal to ______.
In ∆ABC, BC = AB and ∠B = 80°. Then ∠A is equal to ______.
It is given that ∆ABC ≅ ∆FDE and AB = 5 cm, ∠B = 40° and ∠A = 80°. Then which of the following is true?
In a triangle ABC, D is the mid-point of side AC such that BD = `1/2` AC. Show that ∠ABC is a right angle.
