Advertisements
Advertisements
प्रश्न
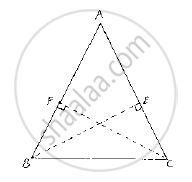
ABC is a triangle in which BE and CF are, respectively, the perpendiculars to the sides AC and AB. If BE = CF, prove that ΔABC is isosceles
उत्तर
Given that ABC is a triangle in which BE and CF are perpendicular to the sides AC and AB respectively such that BE = CF
We have to prove that ΔABC is isosceles
Now, consider ΔBCF and ΔCBE,
We have
∠BFC=CEB=90° [Given]
BC=CB [Common side]
And CF=BE [Given]
So, by RHS congruence criterion, we have ΔBFC≅CEB
Now,
∠FBC=∠EBC [∵ Incongruent triangles corresponding parts are equal]
⇒ ∠ABC=∠ACB
⇒ AC=AB [ ∵Opposite sides to equal angles are equal in a triangle]
∴ ΔABC is isosceles
APPEARS IN
संबंधित प्रश्न
Two lines AB and CD intersect at O such that BC is equal and parallel to AD. Prove that the lines AB and CD bisect at O.
Prove that each angle of an equilateral triangle is 60°.
Which of the following statements are true (T) and which are false (F):
The measure of each angle of an equilateral triangle is 60°
Which of the following statements are true (T) and which are false (F):
The bisectors of two equal angles of a triangle are equal
In a ΔABC, if ∠B = ∠C = 45°, which is the longest side?
Fill in the blank to make the following statement true.
The sum of three altitudes of a triangle is ..... than its perimeter.
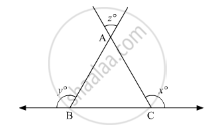
In the given figure, what is z in terms of x and y?
The base BC of triangle ABC is produced both ways and the measure of exterior angles formed are 94° and 126°. Then, ∠BAC =
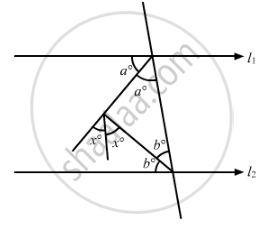
In the given figure, if l1 || l2, the value of x is
In ∆PQR, ∠R = ∠P and QR = 4 cm and PR = 5 cm. Then the length of PQ is ______.
