Advertisements
Advertisements
प्रश्न
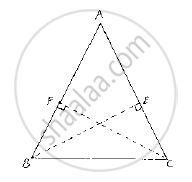
ABC is a triangle in which BE and CF are, respectively, the perpendiculars to the sides AC and AB. If BE = CF, prove that ΔABC is isosceles
Advertisements
उत्तर
Given that ABC is a triangle in which BE and CF are perpendicular to the sides AC and AB respectively such that BE = CF
We have to prove that ΔABC is isosceles
Now, consider ΔBCF and ΔCBE,
We have
∠BFC=CEB=90° [Given]
BC=CB [Common side]
And CF=BE [Given]
So, by RHS congruence criterion, we have ΔBFC≅CEB
Now,
∠FBC=∠EBC [∵ Incongruent triangles corresponding parts are equal]
⇒ ∠ABC=∠ACB
⇒ AC=AB [ ∵Opposite sides to equal angles are equal in a triangle]
∴ ΔABC is isosceles
APPEARS IN
संबंधित प्रश्न
ABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (see the given figure). Show that
- ΔABE ≅ ΔACF
- AB = AC, i.e., ABC is an isosceles triangle.
In Figure AB = AC and ∠ACD =105°, find ∠BAC.
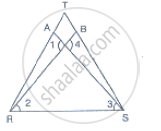
In Fig. 10.40, it is given that RT = TS, ∠1 = 2∠2 and ∠4 = 2∠3. Prove that ΔRBT ≅ ΔSAT
Prove that the medians of an equilateral triangle are equal.
Two lines AB and CD intersect at O such that BC is equal and parallel to AD. Prove that the lines AB and CD bisect at O.
If the bisector of the exterior vertical angle of a triangle be parallel to the base. Show that the triangle is isosceles.
Angles A, B, C of a triangle ABC are equal to each other. Prove that ΔABC is equilateral.
ABC is a triangle in which ∠B = 2 ∠C. D is a point on BC such that AD bisects ∠BAC and AB = CD.
Prove that ∠BAC = 72°.
Which of the following statements are true (T) and which are false (F):
If the bisector of the vertical angle of a triangle bisects the base, then the triangle may be isosceles.
Which of the following statements are true (T) and which are false (F)?
If two angles of a triangle are unequal, then the greater angle has the larger side opposite to it.
Which of the following statements are true (T) and which are false (F)?
Of all the line segments that can be drawn from a point to a line not containing it, the perpendicular line segment is the shortest one.
Fill in the blank to make the following statement true.
Difference of any two sides of a triangle is........ than the third side.
Fill in the blank to make the following statement true.
If two sides of a triangle are unequal, then the larger side has .... angle opposite to it.
In the given figure, if AB || DE and BD || FG such that ∠FGH = 125° and ∠B = 55°, find x and y.
In a ΔABC, if ∠A = 60°, ∠B = 80° and the bisectors of ∠B and ∠C meet at O, then ∠BOC =
In the given figure, if EC || AB, ∠ECD = 70° and ∠BDO = 20°, then ∠OBD is
In a ΔABC, ∠A = 50° and BC is produced to a point D. If the bisectors of ∠ABC and ∠ACDmeet at E, then ∠E =
In ∆ABC, BC = AB and ∠B = 80°. Then ∠A is equal to ______.
In ∆PQR, ∠P = 70° and ∠R = 30°. Which side of this triangle is the longest? Give reason for your answer.
Bisectors of the angles B and C of an isosceles triangle ABC with AB = AC intersect each other at O. Show that external angle adjacent to ∠ABC is equal to ∠BOC
