Advertisements
Advertisements
प्रश्न
Which of the following statements are true (T) and which are false (F) :
If the altitude from one vertex of a triangle bisects the opposite side, then the triangle may be isosceles.
उत्तर
False (F)
Reason: Here the altitude from thee vertex is also the perpendicular bisector of the opposite side.
⇒ The triangle must be isosceles and may be an equilateral triangle.
APPEARS IN
संबंधित प्रश्न
ABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (see the given figure). Show that
- ΔABE ≅ ΔACF
- AB = AC, i.e., ABC is an isosceles triangle.

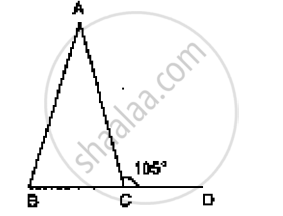
In Figure AB = AC and ∠ACD =105°, find ∠BAC.
If the base of an isosceles triangle is produced on both sides, prove that the exterior angles so formed are equal to each other.
In a ΔABC, if AB = AC and ∠B = 70°, find ∠A.
If the bisector of the exterior vertical angle of a triangle be parallel to the base. Show that the triangle is isosceles.
Prove that each angle of an equilateral triangle is 60°.
Which of the following statements are true (T) and which are false (F)?
Sum of any two sides of a triangle is greater than the third side.
ABC is a triangle. The bisector of the exterior angle at B and the bisector of ∠C intersect each other at D. Prove that ∠D = \[\frac{1}{2}\] ∠A.
In ∆PQR, if ∠R > ∠Q, then ______.
In triangles ABC and PQR, AB = AC, ∠C = ∠P and ∠B = ∠Q. The two triangles are ______.
