Advertisements
Advertisements
प्रश्न
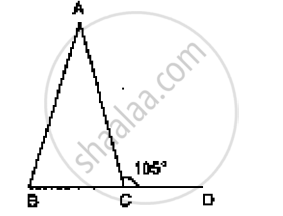
In Figure AB = AC and ∠ACD =105°, find ∠BAC.
उत्तर

Consider the given figure
We have,
AB = AC and ∠ACD =105^@
Since,
∠BCD = 180° = Straight angle
∠BCA + ∠ACD = 180°
∠BCA +105° = 180°
∠BCA = 180° -105° ⇒ ∠BCA = 75° .......1
And also,
ΔABC is an isosceles triangle [∵AB = AC]
⇒ ∠ABC = ∠ACB
From (1), we have [Angles opposite to equal sides are equal]
∠ACB = 75° ⇒∠ABC = ∠ACB = 75°
And also,
Sum of interior angles of a triangle = 180°
⇒∠ABC = ∠BCA + ∠CAB = 180°
⇒ 75° + 75° + ÐCAB = 180°
⇒ 150° +∠BAC = 180°⇒ ∠BAC = 180° -150° = 30°
∠BAC=30°
APPEARS IN
संबंधित प्रश्न
In a ΔABC, if ∠A=l20° and AB = AC. Find ∠B and ∠C.
Find the measure of each exterior angle of an equilateral triangle.
Determine the measure of each of the equal angles of a right-angled isosceles triangle.
In a ΔABC, if ∠A=l20° and AB = AC. Find ∠B and ∠C.
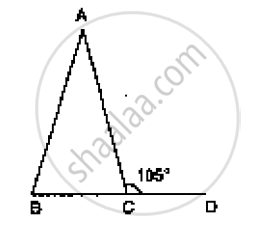
In Figure 10.24, AB = AC and ∠ACD =105°, find ∠BAC.
ABC is a triangle in which ∠B = 2 ∠C. D is a point on BC such that AD bisects ∠BAC and AB = CD.
Prove that ∠BAC = 72°.
Which of the following statements are true (T) and which are false (F)?
Sum of the three sides of a triangle is less than the sum of its three altitudes.
In a triangle ABC, if AB = AC and AB is produced to D such that BD = BC, find ∠ACD: ∠ADC.
The base BC of triangle ABC is produced both ways and the measure of exterior angles formed are 94° and 126°. Then, ∠BAC =
In ∆PQR, ∠P = 70° and ∠R = 30°. Which side of this triangle is the longest? Give reason for your answer.
