Advertisements
Advertisements
प्रश्न
The base BC of triangle ABC is produced both ways and the measure of exterior angles formed are 94° and 126°. Then, ∠BAC =
पर्याय
94°
54°
40°
44°
उत्तर
the given problem, the exterior angles obtained on producing the base of a triangle both ways are 94°and 126°. So, let us draw ΔABC and extend the base BC, such that:
∠ACD = 126°
∠ABE = 94°
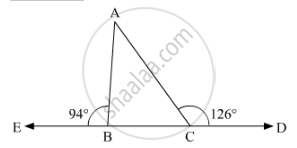
Here, we need to find ∠BAC
Now, since BCD is a straight line, using the property, “angles forming a linear pair are supplementary”, we get
∠ AC+ ∠ ACD = 180°
∠ ACB + 126° = 180°
∠ ACB = 180° - 126°
∠ ACB = 54°
Similarly, EBS is a straight line, so we get,
∠ ABC + ∠ ABE = 180°
∠ ABC + 94° = 180°
∠ ABC = 180° - 94°
∠ ABC = 86°
Further, using angle sum property in ΔABC
∠ ABC + ∠ ACB + ∠ BAC = 180°
54° + 86° + ∠ BAC = 180°
∠ BAC = 180° - 140°
∠ BAC = 40°
Thus, ∠ BAC = 40°
APPEARS IN
संबंधित प्रश्न
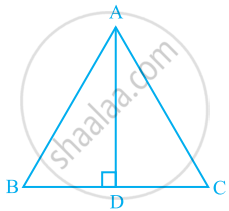
In ΔABC, AD is the perpendicular bisector of BC (see the given figure). Show that ΔABC is an isosceles triangle in which AB = AC.
In a ΔABC, if ∠A=l20° and AB = AC. Find ∠B and ∠C.
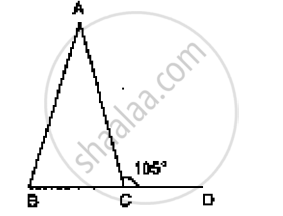
In Figure AB = AC and ∠ACD =105°, find ∠BAC.
BD and CE are bisectors of ∠B and ∠C of an isosceles ΔABC with AB = AC. Prove that BD = CE.
Prove that each angle of an equilateral triangle is 60°.
Fill in the blank to make the following statement true.
Difference of any two sides of a triangle is........ than the third side.
In the given figure, the value of x is ______.
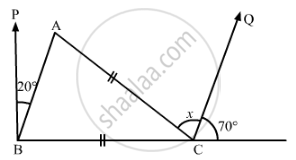
In the given figure, if BP || CQ and AC = BC, then the measure of x is
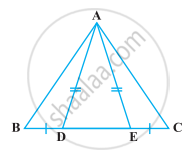
D is a point on the side BC of a ∆ABC such that AD bisects ∠BAC. Then ______.
In the following figure, D and E are points on side BC of a ∆ABC such that BD = CE and AD = AE. Show that ∆ABD ≅ ∆ACE.