Advertisements
Advertisements
प्रश्न
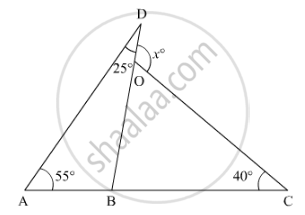
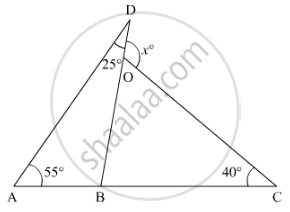
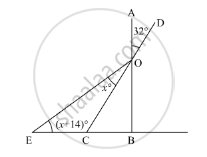
In the given figure, the value of x is ______.
पर्याय
65°
80°
95°
120°
उत्तर
In the given figure, the value of x is 120°.
Explanation:
In the given figure, we need to find the value of x
Here, according to the angle sum property of the triangle
In ΔABD
∠BAD + ∠DBA + ∠ADB = 180°
55° + ∠DBA + 25° = 180°
80 + ∠DBA = 180°
∠DBA = 180° - 80°
∠DBA = 100°
∠DBA = 100°
Also, ABC is a straight line. So, using the property, “angles forming a linear pair are supplementary”, we get,
∠DBA + ∠DBC = 180°
100 + ∠DBC = 180°
∠DBC = 180° - 100°
∠DBC = 80°
Further, using the property, “exterior angle of a triangle is equal to the sum of two opposite interior angles”, we get
ext. ∠DOC + ∠OBC + ∠OCB
x = 80°+ 40°
x = 120°
Thus, x = 120°
APPEARS IN
संबंधित प्रश्न
ABC is an isosceles triangle in which altitudes BE and CF are drawn to equal sides AC and AB respectively (see the given figure). Show that these altitudes are equal.
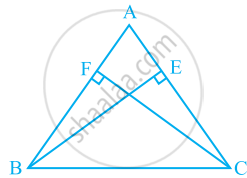
ABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (see the given figure). Show that
- ΔABE ≅ ΔACF
- AB = AC, i.e., ABC is an isosceles triangle.

In figure, AB = AC and DB = DC, find the ratio ∠ABD : ∠ACD
ABC is a right angled triangle in which ∠A = 90° and AB = AC. Find ∠B and ∠C.
Which of the following statements are true (T) and which are false (F)?
Sum of any two sides of a triangle is greater than twice the median drawn to the third side.
In the given figure, if AB ⊥ BC. then x =
In a ΔABC, ∠A = 50° and BC is produced to a point D. If the bisectors of ∠ABC and ∠ACDmeet at E, then ∠E =
D is a point on the side BC of a ∆ABC such that AD bisects ∠BAC. Then ______.
It is given that ∆ABC ≅ ∆FDE and AB = 5 cm, ∠B = 40° and ∠A = 80°. Then which of the following is true?
Two sides of a triangle are of lengths 5 cm and 1.5 cm. The length of the third side of the triangle cannot be ______.
