Advertisements
Advertisements
प्रश्न
In the given figure, what is the value of x?
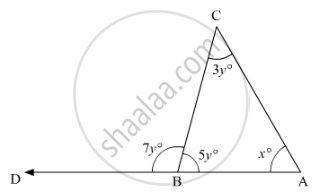
पर्याय
35
45
50
60
उत्तर
In the given figure, we need to find the value of x.
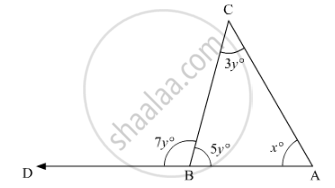
Here, DBA is a straight line, so using the property, “angles forming a linear pair are supplementary”, we get,
∠CBA + ∠CBD = 180°
7y + 5y = 180°
12y = 180°
`y = (180°)/12`
y = 15°
Now, applying the value of y in ∠CBA and ∠BCA
∠BCA = 3y
= 3(15°)
= 45°
Also,
∠CBA = 5y
= 5(15°)
= 75°
Further, applying angle sum property of the triangle
In ΔABC
∠A + ∠B +∠C = 180°
x + 75° + 45° = 180°
x + 120°= 180°
x = 180° - 120°
x = 60°
Thus, x = 60°
APPEARS IN
संबंधित प्रश्न
Find the measure of each exterior angle of an equilateral triangle.
In figure, AB = AC and DB = DC, find the ratio ∠ABD : ∠ACD
In Fig. 10.40, it is given that RT = TS, ∠1 = 2∠2 and ∠4 = 2∠3. Prove that ΔRBT ≅ ΔSAT
In a ΔABC, if ∠B = ∠C = 45°, which is the longest side?
In ΔABC, if ∠A = 40° and ∠B = 60°. Determine the longest and shortest sides of the triangle.
Prove that the perimeter of a triangle is greater than the sum of its altitudes.
In the given figure, if AB || DE and BD || FG such that ∠FGH = 125° and ∠B = 55°, find x and y.
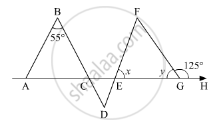
In the given figure, x + y =

The base BC of triangle ABC is produced both ways and the measure of exterior angles formed are 94° and 126°. Then, ∠BAC =
ABC is an isosceles triangle with AB = AC and D is a point on BC such that AD ⊥ BC (Figure). To prove that ∠BAD = ∠CAD, a student proceeded as follows:
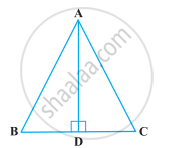
In ∆ABD and ∆ACD,
AB = AC (Given)
∠B = ∠C (Because AB = AC)
and ∠ADB = ∠ADC
Therefore, ∆ABD ≅ ∆ACD (AAS)
So, ∠BAD = ∠CAD (CPCT)
What is the defect in the above arguments?
[Hint: Recall how ∠B = ∠C is proved when AB = AC].
