Advertisements
Advertisements
प्रश्न
In the given figure, what is y in terms of x?

पर्याय
- \[\frac{3}{2}x\]
- \[\frac{4}{3}x\]
- x
\[\frac{3}{4}x\]
उत्तर
In the given figure, we need to find y in terms of x

Now, using the property, “an exterior angle of the triangle is equal to the sum of the two opposite interior angles”, we get
In ΔABC
ext∠ACD = ∠CAB + ∠CBA
ext∠ACD = x + 2x
ext∠ACD =3x ..........(1)
Similarly, in ΔOCD
ext∠AOD = ∠OCD + ∠CDO
3y = ∠OCD + y (using 1)
3y - y = 3x
2y = 3x
`y = 3/2 x`
Thus, `y = 3/2x `
APPEARS IN
संबंधित प्रश्न
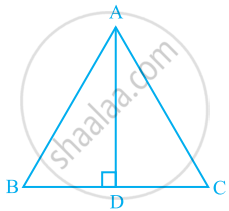
In ΔABC, AD is the perpendicular bisector of BC (see the given figure). Show that ΔABC is an isosceles triangle in which AB = AC.
Show that the angles of an equilateral triangle are 60° each.
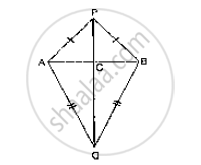
AB is a line seg P and Q are points on opposite sides of AB such that each of them is equidistant from the points A and B (See Fig. 10.26). Show that the line PQ is perpendicular bisector of AB.
ABC is a right angled triangle in which ∠A = 90° and AB = AC. Find ∠B and ∠C.
Which of the following statements are true (T) and which are false (F)?
Difference of any two sides of a triangle is equal to the third side.
Fill in the blank to make the following statement true.
The sum of any two sides of a triangle is .... than the third side.
In the given figure, the value of x is ______.
In the given figure, AB and CD are parallel lines and transversal EF intersects them at Pand Q respectively. If ∠APR = 25°, ∠RQC = 30° and ∠CQF = 65°, then

The side BC of ΔABC is produced to a point D. The bisector of ∠A meets side BC in L. If ∠ABC = 30° and ∠ACD = 115°, then ∠ALC = ______.
In triangles ABC and PQR, AB = AC, ∠C = ∠P and ∠B = ∠Q. The two triangles are ______.
