Question

AB is a line seg P and Q are points on opposite sides of AB such that each of them is equidistant from the points A and B (See Fig. 10.26). Show that the line PQ is perpendicular bisector of AB. 

 

Answer 1

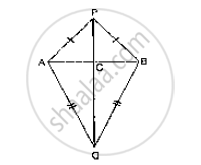
Consider the figure,

We have

AB is a line segment and P,Q are points on opposite sides of AB such that

AP = BP           .......(1)

AQ = BQ          ........(2)

We have to prove that PQ is perpendicular bisector of AB. Now consider DPAQ and DPBQ, 

We have  AP = BP            [∵ From (1)]

AQ = BQ                          [∵ From (2)]

And PQ = PQ                  [Common site] 

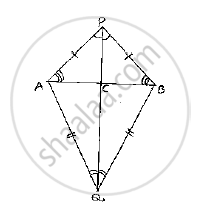
⇒∠PAQ ≅ ∠PBQ               ..….(3)           [From SSS congruence] 

Now, we can observe that Δ𝐴𝑃𝐵 𝑎𝑛𝑑 Δ𝐴𝐵𝑄 are isosceles triangles.(From 1 and 2)

⟹∠𝑃𝐴𝐵 = ∠𝑃𝐵𝐴 𝑎𝑛𝑑 ∠𝑄𝐴𝐵 = ∠𝑄𝐵𝐴 

Now consider ΔPAC and , ΔPBC
C is the point of intersection of AB and PQ.

PA = PB                          [from (1)] 

∠APC = ∠BPC               [from (2)]

PC = PC                        [Common side] 

So, from SAS congruency of triangle ΔPAC ≅  ΔPBC

⇒AC = CB and∠PCA = ∠PCB         …….(4)

[∵ Corresponding parts of congruent triangles are equal] And also, ACB is line segment

⇒∠ACP + ∠BCP = 180°

But ∠ACP =∠PCB

⇒∠ACP = ∠PCB = 90°                        ………(5)

We have AC = CB ⇒ C is the midpoint of AB

From (4) and (5)

We can conclude that PC is the perpendicular bisector of AB

Since C is a point on the line PQ, we can say that PQ is the perpendicular bisector of AB.