Advertisements
Advertisements
प्रश्न
Two lines AB and CD intersect at O such that BC is equal and parallel to AD. Prove that the lines AB and CD bisect at O.
उत्तर
It is given that
BC = AD
BC || AD
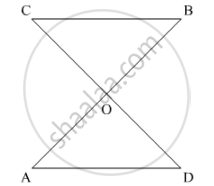
We have to prove that AB and CD bisect at O.
If we prove that ΔAOD ≅ ΔBOC , then
We can prove AB and CDbisects atO.
Now in ΔAOD and ΔBOC
AD = BC(Given)
∠OBC =∠OAD (Since AD || BC and AB is transversal)
And ∠OCB = ∠ODA(since AD || BC and CD is transversal)
So by ASAcongruence criterion we have,
ΔAOD ≅ ΔBOC, so
OA = OB
OD = OC
Hence ABand CD bisect each other at O.
APPEARS IN
संबंधित प्रश्न
In an isosceles triangle ABC, with AB = AC, the bisectors of ∠B and ∠C intersect each other at O. Join A to O. Show that:
- OB = OC
- AO bisects ∠A
In figure, AB = AC and DB = DC, find the ratio ∠ABD : ∠ACD
In a ΔABC, if AB = AC and ∠B = 70°, find ∠A.
Fill the blank in the following so that the following statement is true.
Sides opposite to equal angles of a triangle are ......
In a ΔABC, if ∠B = ∠C = 45°, which is the longest side?
Fill in the blank to make the following statement true.
Difference of any two sides of a triangle is........ than the third side.
In a ΔABC, ∠A = 50° and BC is produced to a point D. If the bisectors of ∠ABC and ∠ACDmeet at E, then ∠E =
In ∆ABC, BC = AB and ∠B = 80°. Then ∠A is equal to ______.
Show that in a quadrilateral ABCD, AB + BC + CD + DA < 2(BD + AC)
In a triangle ABC, D is the mid-point of side AC such that BD = `1/2` AC. Show that ∠ABC is a right angle.
