Advertisements
Advertisements
प्रश्न
Show that in a quadrilateral ABCD, AB + BC + CD + DA < 2(BD + AC)
उत्तर
Given: ABCD is a quadrilateral.
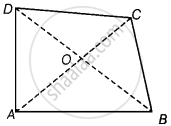
To show: AB + BC + CD + DA < 2(BD + AC)
Construction: Join diagonals AC and BD.
Proof: In ΔOAB, OA + OB > AB ...(i) [Sum of two sides of a triangle is greater than the third side]
In ΔOBC, OB + OC > BC ...(ii) [Sum of two sides of a triangle is greater than the third side]
In ΔOCD, OC + OD > CD ...(iii) [Sum of two sides of a triangle is greater than the third side]
In ΔODA, OD + OA > DA ...(iv) [Sum of two sides of a triangle is greater than the third side]
On adding equations (i), (ii), (iii) and (iv), we get
2[(OA + OB + OC + OD] > AB + BC + CD + DA
⇒ 2[(OA + OC) + (OB + OD)] > AB + BC + CD + DA
⇒ 2(AC + BD) > AB + BC + CD + DA ...[∵ OA + OC = AC and OB + OD = BD]
⇒ AB + BC + CD + DA < 2(BD + AC)
APPEARS IN
संबंधित प्रश्न
ABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (see the given figure). Show that
- ΔABE ≅ ΔACF
- AB = AC, i.e., ABC is an isosceles triangle.

If the bisector of the exterior vertical angle of a triangle be parallel to the base. Show that the triangle is isosceles.
Which of the following statements are true (T) and which are false (F):
Angles opposite to equal sides of a triangle are equal
Which of the following statements are true (T) and which are false (F):
The two altitudes corresponding to two equal sides of a triangle need not be equal.
Fill the blank in the following so that the following statement is true.
In an isosceles triangle ABC with AB = AC, if BD and CE are its altitudes, then BD is …… CE.
Fill in the blank to make the following statement true.
If two angles of a triangle are unequal, then the smaller angle has the........ side opposite to it.
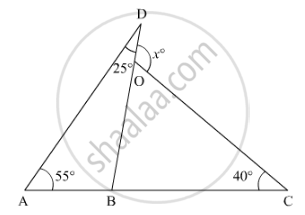
In the given figure, the value of x is ______.
In ∆ABC, AB = AC and ∠B = 50°. Then ∠C is equal to ______.
In ∆PQR, ∠R = ∠P and QR = 4 cm and PR = 5 cm. Then the length of PQ is ______.
Is it possible to construct a triangle with lengths of its sides as 9 cm, 7 cm and 17 cm? Give reason for your answer.
