Advertisements
Advertisements
प्रश्न
Show that in a quadrilateral ABCD, AB + BC + CD + DA > AC + BD
उत्तर
Given in the question, a quadrilateral ABCD.
To proof that AB + BC + CD + DA > AC + BD.
Proof: In triangle ABC,

AB + BC > AC ...(i) [Sum of the lengths of any two sides of a triangle must be greater than the third side]
In triangle BCD,
BC + CD > BD ...(ii) [Sum of the lengths of any two sides of a triangle must be greater than the third side]
In triangle CDA,
CD + DA > AC ...(iii) [Sum of the lengths of any two sides of a triangle must be greater than the third side]
Similarly, in triangle DAB,
AD + AB > BD ...(iv) [Sum of the lengths of any two sides of a triangle must be greater than the third side]
Now, adding equation (i), (ii), (iii) and (iv), we get
AB + BC + BC + CD + CD + DA + AD + AB > AC + BD + AC + BD
2AB + 2BC + 2CD > 2AC + 2BD
2(AB + BC + CD + DA) > 2(AC + BD)
AB + BC + CD + DA > AC + BD
Hence proved.
APPEARS IN
संबंधित प्रश्न
Show that the angles of an equilateral triangle are 60° each.
Find the measure of each exterior angle of an equilateral triangle.
Which of the following statements are true (T) and which are false (F):
Sides opposite to equal angles of a triangle may be unequal
Fill the blank in the following so that the following statement is true.
Angle opposite to equal sides of a triangle are .....
Fill the blank in the following so that the following statement is true.
In a ΔABC if ∠A = ∠C , then AB = ......
In a triangle ABC, if AB = AC and AB is produced to D such that BD = BC, find ∠ACD: ∠ADC.
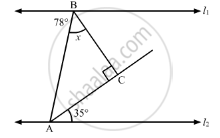
In the given figure, for which value of x is l1 || l2?
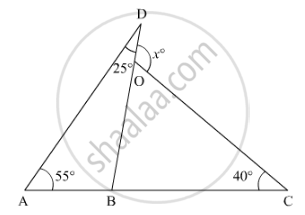
In the given figure, the value of x is ______.
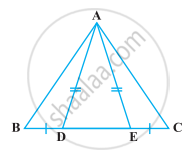
AD is a median of the triangle ABC. Is it true that AB + BC + CA > 2AD? Give reason for your answer.
In the following figure, D and E are points on side BC of a ∆ABC such that BD = CE and AD = AE. Show that ∆ABD ≅ ∆ACE.