Advertisements
Advertisements
Question
Show that in a quadrilateral ABCD, AB + BC + CD + DA > AC + BD
Solution
Given in the question, a quadrilateral ABCD.
To proof that AB + BC + CD + DA > AC + BD.
Proof: In triangle ABC,

AB + BC > AC ...(i) [Sum of the lengths of any two sides of a triangle must be greater than the third side]
In triangle BCD,
BC + CD > BD ...(ii) [Sum of the lengths of any two sides of a triangle must be greater than the third side]
In triangle CDA,
CD + DA > AC ...(iii) [Sum of the lengths of any two sides of a triangle must be greater than the third side]
Similarly, in triangle DAB,
AD + AB > BD ...(iv) [Sum of the lengths of any two sides of a triangle must be greater than the third side]
Now, adding equation (i), (ii), (iii) and (iv), we get
AB + BC + BC + CD + CD + DA + AD + AB > AC + BD + AC + BD
2AB + 2BC + 2CD > 2AC + 2BD
2(AB + BC + CD + DA) > 2(AC + BD)
AB + BC + CD + DA > AC + BD
Hence proved.
APPEARS IN
RELATED QUESTIONS
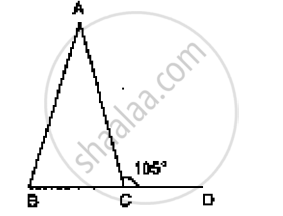
In Figure AB = AC and ∠ACD =105°, find ∠BAC.
ABC is a triangle. The bisector of the exterior angle at B and the bisector of ∠C intersect each other at D. Prove that ∠D = \[\frac{1}{2}\] ∠A.
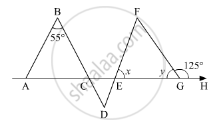
In the given figure, if AB || DE and BD || FG such that ∠FGH = 125° and ∠B = 55°, find x and y.
If the angles A, B and C of ΔABC satisfy the relation B − A = C − B, then find the measure of ∠B.
In the given figure, x + y =

The base BC of triangle ABC is produced both ways and the measure of exterior angles formed are 94° and 126°. Then, ∠BAC =
In ∆ABC, AB = AC and ∠B = 50°. Then ∠C is equal to ______.
Two sides of a triangle are of lengths 5 cm and 1.5 cm. The length of the third side of the triangle cannot be ______.
If ∆PQR ≅ ∆EDF, then is it true to say that PR = EF? Give reason for your answer
In ∆PQR, ∠P = 70° and ∠R = 30°. Which side of this triangle is the longest? Give reason for your answer.
