Advertisements
Advertisements
Question
ABC is a triangle. The bisector of the exterior angle at B and the bisector of ∠C intersect each other at D. Prove that ∠D = \[\frac{1}{2}\] ∠A.
Solution
In the given ΔABC, the bisectors of ext,∠B and ∠Cntersect at D
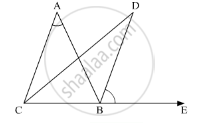
We need to prove: `∠D = 1/2 ∠A`
Now, using the exterior angle theorem,
\[\angle ABE = \angle BAC + \angle ACB\] .….(1)
\[As \angle \text {ABE and } \angle \text { ACB are bisected }\]
\[\angle DCB = \frac{1}{2}\angle ACB\]
Also,
\[\angle DBA = \frac{1}{2}\angle ABE\]
Further, applying angle sum property of the triangle
In ΔDCB
\[\angle CDB + \angle DCB + \angle CBD = 180^\circ\]
\[ \Rightarrow \angle CDB + \frac{1}{2}\angle ACB + \left( \angle DBA + \angle ABC \right) = 180^\circ\]
\[\angle CDB + \frac{1}{2}\angle ACB + \left( \frac{1}{2}\angle ABE + \angle ABC \right) = 180^\circ . . . . . \left( 2 \right)\]
Also, CBE is a straight line, So, using linear pair property
\[\Rightarrow \angle ABC + \angle ABE = 180^\circ\]
\[ \Rightarrow \angle ABC + \frac{1}{2}\angle ABE + \frac{1}{2}\angle ABE = 180^\circ \]
\[ \Rightarrow \angle ABC + \frac{1}{2}\angle ABE = 180^\circ - \frac{1}{2}\angle ABE . . . . . \left( 3 \right)\]
So, using (3) in (2)
\[\angle CDB + \frac{1}{2}\angle ACB + \left( 180^\circ - \frac{1}{2}\angle ABE \right) = 180^\circ \]
\[ \Rightarrow \angle CDB + \frac{1}{2}\angle ACB - \frac{1}{2}\angle ABE = 0\]
\[ \Rightarrow \angle CDB = \frac{1}{2}\left( \angle ABE - \angle ACB \right)\]
\[ \Rightarrow \angle CDB = \frac{1}{2}\angle CAB\]
\[ \Rightarrow \angle D = \frac{1}{2}\angle A\]
Hence proved.
APPEARS IN
RELATED QUESTIONS
Prove that the medians of an equilateral triangle are equal.
The vertical angle of an isosceles triangle is 100°. Find its base angles.
Which of the following statements are true (T) and which are false (F) :
If the altitude from one vertex of a triangle bisects the opposite side, then the triangle may be isosceles.
Fill in the blank to make the following statement true.
The sum of three altitudes of a triangle is ..... than its perimeter.
In ΔABC, if ∠A = 100°, AD bisects ∠A and AD ⊥ BC. Then, ∠B =
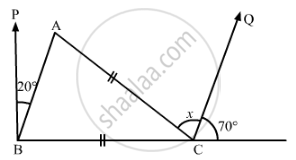
In the given figure, if BP || CQ and AC = BC, then the measure of x is
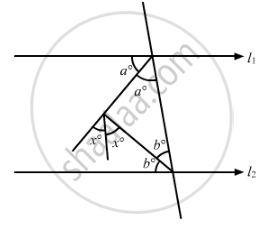
In the given figure, if l1 || l2, the value of x is
The angles of a right angled triangle are
Two sides of a triangle are of lengths 5 cm and 1.5 cm. The length of the third side of the triangle cannot be ______.
Is it possible to construct a triangle with lengths of its sides as 9 cm, 7 cm and 17 cm? Give reason for your answer.
